/* CubicCurve2D.java -- represents a parameterized cubic curve in 2-D space
Copyright (C) 2002, 2003, 2004 Free Software Foundation
This file is part of GNU Classpath.
GNU Classpath is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 2, or (at your option)
any later version.
GNU Classpath is distributed in the hope that it will be useful, but
WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU
General Public License for more details.
You should have received a copy of the GNU General Public License
along with GNU Classpath; see the file COPYING. If not, write to the
Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA
02110-1301 USA.
Linking this library statically or dynamically with other modules is
making a combined work based on this library. Thus, the terms and
conditions of the GNU General Public License cover the whole
combination.
As a special exception, the copyright holders of this library give you
permission to link this library with independent modules to produce an
executable, regardless of the license terms of these independent
modules, and to copy and distribute the resulting executable under
terms of your choice, provided that you also meet, for each linked
independent module, the terms and conditions of the license of that
module. An independent module is a module which is not derived from
or based on this library. If you modify this library, you may extend
this exception to your version of the library, but you are not
obligated to do so. If you do not wish to do so, delete this
exception statement from your version. */
package java.awt.geom;
import java.awt.Rectangle;
import java.awt.Shape;
import java.util.NoSuchElementException;
/**
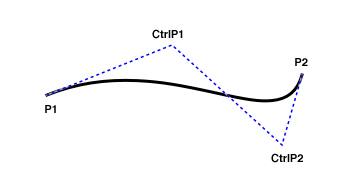
* A two-dimensional curve that is parameterized with a cubic
* function.
*
* 
*
* @author Eric Blake (ebb9@email.byu.edu)
* @author Graydon Hoare (graydon@redhat.com)
* @author Sascha Brawer (brawer@dandelis.ch)
* @author Sven de Marothy (sven@physto.se)
*
* @since 1.2
*/
public abstract class CubicCurve2D implements Shape, Cloneable
{
private static final double BIG_VALUE = java.lang.Double.MAX_VALUE / 10.0;
private static final double EPSILON = 1E-10;
/**
* Constructs a new CubicCurve2D. Typical users will want to
* construct instances of a subclass, such as {@link
* CubicCurve2D.Float} or {@link CubicCurve2D.Double}.
*/
protected CubicCurve2D()
{
}
/**
* Returns the x coordinate of the curve’s start
* point.
*/
public abstract double getX1();
/**
* Returns the y coordinate of the curve’s start
* point.
*/
public abstract double getY1();
/**
* Returns the curve’s start point.
*/
public abstract Point2D getP1();
/**
* Returns the x coordinate of the curve’s first
* control point.
*/
public abstract double getCtrlX1();
/**
* Returns the y coordinate of the curve’s first
* control point.
*/
public abstract double getCtrlY1();
/**
* Returns the curve’s first control point.
*/
public abstract Point2D getCtrlP1();
/**
* Returns the x coordinate of the curve’s second
* control point.
*/
public abstract double getCtrlX2();
/**
* Returns the y coordinate of the curve’s second
* control point.
*/
public abstract double getCtrlY2();
/**
* Returns the curve’s second control point.
*/
public abstract Point2D getCtrlP2();
/**
* Returns the x coordinate of the curve’s end
* point.
*/
public abstract double getX2();
/**
* Returns the y coordinate of the curve’s end
* point.
*/
public abstract double getY2();
/**
* Returns the curve’s end point.
*/
public abstract Point2D getP2();
/**
* Changes the curve geometry, separately specifying each coordinate
* value.
*
*
*
* @param x1 the x coordinate of the curve’s new start
* point.
*
* @param y1 the y coordinate of the curve’s new start
* point.
*
* @param cx1 the x coordinate of the curve’s new
* first control point.
*
* @param cy1 the y coordinate of the curve’s new
* first control point.
*
* @param cx2 the x coordinate of the curve’s new
* second control point.
*
* @param cy2 the y coordinate of the curve’s new
* second control point.
*
* @param x2 the x coordinate of the curve’s new end
* point.
*
* @param y2 the y coordinate of the curve’s new end
* point.
*/
public abstract void setCurve(double x1, double y1, double cx1, double cy1,
double cx2, double cy2, double x2, double y2);
/**
* Changes the curve geometry, specifying coordinate values in an
* array.
*
* @param coords an array containing the new coordinate values. The
* x coordinate of the new start point is located at
* coords[offset], its y coordinate at
* coords[offset + 1]. The x coordinate of the
* new first control point is located at coords[offset +
* 2], its y coordinate at coords[offset +
* 3]. The x coordinate of the new second control
* point is located at coords[offset + 4], its y
* coordinate at coords[offset + 5]. The x
* coordinate of the new end point is located at coords[offset
* + 6], its y coordinate at coords[offset +
* 7].
*
* @param offset the offset of the first coordinate value in
* coords.
*/
public void setCurve(double[] coords, int offset)
{
setCurve(coords[offset++], coords[offset++], coords[offset++],
coords[offset++], coords[offset++], coords[offset++],
coords[offset++], coords[offset++]);
}
/**
* Changes the curve geometry, specifying coordinate values in
* separate Point objects.
*
*
*
*
The curve does not keep any reference to the passed point
* objects. Therefore, a later change to p1,
* c1, c2 or p2 will not
* affect the curve geometry.
*
* @param p1 the new start point.
* @param c1 the new first control point.
* @param c2 the new second control point.
* @param p2 the new end point.
*/
public void setCurve(Point2D p1, Point2D c1, Point2D c2, Point2D p2)
{
setCurve(p1.getX(), p1.getY(), c1.getX(), c1.getY(), c2.getX(), c2.getY(),
p2.getX(), p2.getY());
}
/**
* Changes the curve geometry, specifying coordinate values in an
* array of Point objects.
*
*
*
*
The curve does not keep references to the passed point
* objects. Therefore, a later change to the pts array
* or any of its elements will not affect the curve geometry.
*
* @param pts an array containing the points. The new start point
* is located at pts[offset], the new first control
* point at pts[offset + 1], the new second control
* point at pts[offset + 2], and the new end point
* at pts[offset + 3].
*
* @param offset the offset of the start point in pts.
*/
public void setCurve(Point2D[] pts, int offset)
{
setCurve(pts[offset].getX(), pts[offset++].getY(), pts[offset].getX(),
pts[offset++].getY(), pts[offset].getX(), pts[offset++].getY(),
pts[offset].getX(), pts[offset++].getY());
}
/**
* Changes the curve geometry to that of another curve.
*
* @param c the curve whose coordinates will be copied.
*/
public void setCurve(CubicCurve2D c)
{
setCurve(c.getX1(), c.getY1(), c.getCtrlX1(), c.getCtrlY1(),
c.getCtrlX2(), c.getCtrlY2(), c.getX2(), c.getY2());
}
/**
* Calculates the squared flatness of a cubic curve, directly
* specifying each coordinate value. The flatness is the maximal
* distance of a control point to the line between start and end
* point.
*
*
*
*
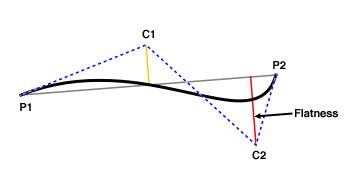
In the above drawing, the straight line connecting start point
* P1 and end point P2 is depicted in gray. In comparison to C1,
* control point C2 is father away from the gray line. Therefore,
* the result will be the square of the distance between C2 and the
* gray line, i.e. the squared length of the red line.
*
* @param x1 the x coordinate of the start point P1.
* @param y1 the y coordinate of the start point P1.
* @param cx1 the x coordinate of the first control point C1.
* @param cy1 the y coordinate of the first control point C1.
* @param cx2 the x coordinate of the second control point C2.
* @param cy2 the y coordinate of the second control point C2.
* @param x2 the x coordinate of the end point P2.
* @param y2 the y coordinate of the end point P2.
*/
public static double getFlatnessSq(double x1, double y1, double cx1,
double cy1, double cx2, double cy2,
double x2, double y2)
{
return Math.max(Line2D.ptSegDistSq(x1, y1, x2, y2, cx1, cy1),
Line2D.ptSegDistSq(x1, y1, x2, y2, cx2, cy2));
}
/**
* Calculates the flatness of a cubic curve, directly specifying
* each coordinate value. The flatness is the maximal distance of a
* control point to the line between start and end point.
*
*
*
*
In the above drawing, the straight line connecting start point
* P1 and end point P2 is depicted in gray. In comparison to C1,
* control point C2 is father away from the gray line. Therefore,
* the result will be the distance between C2 and the gray line,
* i.e. the length of the red line.
*
* @param x1 the x coordinate of the start point P1.
* @param y1 the y coordinate of the start point P1.
* @param cx1 the x coordinate of the first control point C1.
* @param cy1 the y coordinate of the first control point C1.
* @param cx2 the x coordinate of the second control point C2.
* @param cy2 the y coordinate of the second control point C2.
* @param x2 the x coordinate of the end point P2.
* @param y2 the y coordinate of the end point P2.
*/
public static double getFlatness(double x1, double y1, double cx1,
double cy1, double cx2, double cy2,
double x2, double y2)
{
return Math.sqrt(getFlatnessSq(x1, y1, cx1, cy1, cx2, cy2, x2, y2));
}
/**
* Calculates the squared flatness of a cubic curve, specifying the
* coordinate values in an array. The flatness is the maximal
* distance of a control point to the line between start and end
* point.
*
*
*
*
In the above drawing, the straight line connecting start point
* P1 and end point P2 is depicted in gray. In comparison to C1,
* control point C2 is father away from the gray line. Therefore,
* the result will be the square of the distance between C2 and the
* gray line, i.e. the squared length of the red line.
*
* @param coords an array containing the coordinate values. The
* x coordinate of the start point P1 is located at
* coords[offset], its y coordinate at
* coords[offset + 1]. The x coordinate of the
* first control point C1 is located at coords[offset +
* 2], its y coordinate at coords[offset +
* 3]. The x coordinate of the second control point C2
* is located at coords[offset + 4], its y
* coordinate at coords[offset + 5]. The x
* coordinate of the end point P2 is located at coords[offset
* + 6], its y coordinate at coords[offset +
* 7].
*
* @param offset the offset of the first coordinate value in
* coords.
*/
public static double getFlatnessSq(double[] coords, int offset)
{
return getFlatnessSq(coords[offset++], coords[offset++], coords[offset++],
coords[offset++], coords[offset++], coords[offset++],
coords[offset++], coords[offset++]);
}
/**
* Calculates the flatness of a cubic curve, specifying the
* coordinate values in an array. The flatness is the maximal
* distance of a control point to the line between start and end
* point.
*
*
*
*
In the above drawing, the straight line connecting start point
* P1 and end point P2 is depicted in gray. In comparison to C1,
* control point C2 is father away from the gray line. Therefore,
* the result will be the distance between C2 and the gray line,
* i.e. the length of the red line.
*
* @param coords an array containing the coordinate values. The
* x coordinate of the start point P1 is located at
* coords[offset], its y coordinate at
* coords[offset + 1]. The x coordinate of the
* first control point C1 is located at coords[offset +
* 2], its y coordinate at coords[offset +
* 3]. The x coordinate of the second control point C2
* is located at coords[offset + 4], its y
* coordinate at coords[offset + 5]. The x
* coordinate of the end point P2 is located at coords[offset
* + 6], its y coordinate at coords[offset +
* 7].
*
* @param offset the offset of the first coordinate value in
* coords.
*/
public static double getFlatness(double[] coords, int offset)
{
return Math.sqrt(getFlatnessSq(coords[offset++], coords[offset++],
coords[offset++], coords[offset++],
coords[offset++], coords[offset++],
coords[offset++], coords[offset++]));
}
/**
* Calculates the squared flatness of this curve. The flatness is
* the maximal distance of a control point to the line between start
* and end point.
*
*
*
*
In the above drawing, the straight line connecting start point
* P1 and end point P2 is depicted in gray. In comparison to C1,
* control point C2 is father away from the gray line. Therefore,
* the result will be the square of the distance between C2 and the
* gray line, i.e. the squared length of the red line.
*/
public double getFlatnessSq()
{
return getFlatnessSq(getX1(), getY1(), getCtrlX1(), getCtrlY1(),
getCtrlX2(), getCtrlY2(), getX2(), getY2());
}
/**
* Calculates the flatness of this curve. The flatness is the
* maximal distance of a control point to the line between start and
* end point.
*
*
*
*
In the above drawing, the straight line connecting start point
* P1 and end point P2 is depicted in gray. In comparison to C1,
* control point C2 is father away from the gray line. Therefore,
* the result will be the distance between C2 and the gray line,
* i.e. the length of the red line.
*/
public double getFlatness()
{
return Math.sqrt(getFlatnessSq(getX1(), getY1(), getCtrlX1(), getCtrlY1(),
getCtrlX2(), getCtrlY2(), getX2(), getY2()));
}
/**
* Subdivides this curve into two halves.
*
*
*
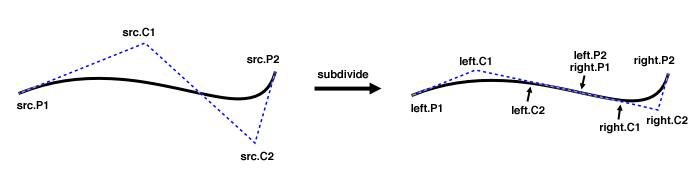* @param left a curve whose geometry will be set to the left half
* of this curve, or null if the caller is not
* interested in the left half.
*
* @param right a curve whose geometry will be set to the right half
* of this curve, or null if the caller is not
* interested in the right half.
*/
public void subdivide(CubicCurve2D left, CubicCurve2D right)
{
// Use empty slots at end to share single array.
double[] d = new double[]
{
getX1(), getY1(), getCtrlX1(), getCtrlY1(), getCtrlX2(),
getCtrlY2(), getX2(), getY2(), 0, 0, 0, 0, 0, 0
};
subdivide(d, 0, d, 0, d, 6);
if (left != null)
left.setCurve(d, 0);
if (right != null)
right.setCurve(d, 6);
}
/**
* Subdivides a cubic curve into two halves.
*
*
*
* @param src the curve to be subdivided.
*
* @param left a curve whose geometry will be set to the left half
* of src, or null if the caller is not
* interested in the left half.
*
* @param right a curve whose geometry will be set to the right half
* of src, or null if the caller is not
* interested in the right half.
*/
public static void subdivide(CubicCurve2D src, CubicCurve2D left,
CubicCurve2D right)
{
src.subdivide(left, right);
}
/**
* Subdivides a cubic curve into two halves, passing all coordinates
* in an array.
*
*
*
*
The left end point and the right start point will always be
* identical. Memory-concious programmers thus may want to pass the
* same array for both left and right, and
* set rightOff to leftOff + 6.
*
* @param src an array containing the coordinates of the curve to be
* subdivided. The x coordinate of the start point P1 is
* located at src[srcOff], its y at
* src[srcOff + 1]. The x coordinate of the
* first control point C1 is located at src[srcOff +
* 2], its y at src[srcOff + 3]. The
* x coordinate of the second control point C2 is located at
* src[srcOff + 4], its y at src[srcOff +
* 5]. The x coordinate of the end point is located at
* src[srcOff + 6], its y at src[srcOff +
* 7].
*
* @param srcOff an offset into src, specifying
* the index of the start point’s x coordinate.
*
* @param left an array that will receive the coordinates of the
* left half of src. It is acceptable to pass
* src. A caller who is not interested in the left half
* can pass null.
*
* @param leftOff an offset into left, specifying the
* index where the start point’s x coordinate will be
* stored.
*
* @param right an array that will receive the coordinates of the
* right half of src. It is acceptable to pass
* src or left. A caller who is not
* interested in the right half can pass null.
*
* @param rightOff an offset into right, specifying the
* index where the start point’s x coordinate will be
* stored.
*/
public static void subdivide(double[] src, int srcOff, double[] left,
int leftOff, double[] right, int rightOff)
{
// To understand this code, please have a look at the image
// "CubicCurve2D-3.png" in the sub-directory "doc-files".
double src_C1_x;
double src_C1_y;
double src_C2_x;
double src_C2_y;
double left_P1_x;
double left_P1_y;
double left_C1_x;
double left_C1_y;
double left_C2_x;
double left_C2_y;
double right_C1_x;
double right_C1_y;
double right_C2_x;
double right_C2_y;
double right_P2_x;
double right_P2_y;
double Mid_x; // Mid = left.P2 = right.P1
double Mid_y; // Mid = left.P2 = right.P1
left_P1_x = src[srcOff];
left_P1_y = src[srcOff + 1];
src_C1_x = src[srcOff + 2];
src_C1_y = src[srcOff + 3];
src_C2_x = src[srcOff + 4];
src_C2_y = src[srcOff + 5];
right_P2_x = src[srcOff + 6];
right_P2_y = src[srcOff + 7];
left_C1_x = (left_P1_x + src_C1_x) / 2;
left_C1_y = (left_P1_y + src_C1_y) / 2;
right_C2_x = (right_P2_x + src_C2_x) / 2;
right_C2_y = (right_P2_y + src_C2_y) / 2;
Mid_x = (src_C1_x + src_C2_x) / 2;
Mid_y = (src_C1_y + src_C2_y) / 2;
left_C2_x = (left_C1_x + Mid_x) / 2;
left_C2_y = (left_C1_y + Mid_y) / 2;
right_C1_x = (Mid_x + right_C2_x) / 2;
right_C1_y = (Mid_y + right_C2_y) / 2;
Mid_x = (left_C2_x + right_C1_x) / 2;
Mid_y = (left_C2_y + right_C1_y) / 2;
if (left != null)
{
left[leftOff] = left_P1_x;
left[leftOff + 1] = left_P1_y;
left[leftOff + 2] = left_C1_x;
left[leftOff + 3] = left_C1_y;
left[leftOff + 4] = left_C2_x;
left[leftOff + 5] = left_C2_y;
left[leftOff + 6] = Mid_x;
left[leftOff + 7] = Mid_y;
}
if (right != null)
{
right[rightOff] = Mid_x;
right[rightOff + 1] = Mid_y;
right[rightOff + 2] = right_C1_x;
right[rightOff + 3] = right_C1_y;
right[rightOff + 4] = right_C2_x;
right[rightOff + 5] = right_C2_y;
right[rightOff + 6] = right_P2_x;
right[rightOff + 7] = right_P2_y;
}
}
/**
* Finds the non-complex roots of a cubic equation, placing the
* results into the same array as the equation coefficients. The
* following equation is being solved:
*
*
eqn[3] · x3
* + eqn[2] · x2
* + eqn[1] · x
* + eqn[0]
* = 0
*
*
* For some background about solving cubic equations, see the
* article “Cubic Formula” in PlanetMath. For an extensive
* library of numerical algorithms written in the C programming
* language, see the GNU
* Scientific Library, from which this implementation was
* adapted.
*
* @param eqn an array with the coefficients of the equation. When
* this procedure has returned, eqn will contain the
* non-complex solutions of the equation, in no particular order.
*
* @return the number of non-complex solutions. A result of 0
* indicates that the equation has no non-complex solutions. A
* result of -1 indicates that the equation is constant (i.e.,
* always or never zero).
*
* @see #solveCubic(double[], double[])
* @see QuadCurve2D#solveQuadratic(double[],double[])
*
* @author Brian Gough (bjg@network-theory.com)
* (original C implementation in the GNU Scientific Library)
*
* @author Sascha Brawer (brawer@dandelis.ch)
* (adaptation to Java)
*/
public static int solveCubic(double[] eqn)
{
return solveCubic(eqn, eqn);
}
/**
* Finds the non-complex roots of a cubic equation. The following
* equation is being solved:
*
*
eqn[3] · x3
* + eqn[2] · x2
* + eqn[1] · x
* + eqn[0]
* = 0
*
*
* For some background about solving cubic equations, see the
* article “Cubic Formula” in PlanetMath. For an extensive
* library of numerical algorithms written in the C programming
* language, see the GNU
* Scientific Library, from which this implementation was
* adapted.
*
* @see QuadCurve2D#solveQuadratic(double[],double[])
*
* @param eqn an array with the coefficients of the equation.
*
* @param res an array into which the non-complex roots will be
* stored. The results may be in an arbitrary order. It is safe to
* pass the same array object reference for both eqn
* and res.
*
* @return the number of non-complex solutions. A result of 0
* indicates that the equation has no non-complex solutions. A
* result of -1 indicates that the equation is constant (i.e.,
* always or never zero).
*
* @author Brian Gough (bjg@network-theory.com)
* (original C implementation in the GNU Scientific Library)
*
* @author Sascha Brawer (brawer@dandelis.ch)
* (adaptation to Java)
*/
public static int solveCubic(double[] eqn, double[] res)
{
// Adapted from poly/solve_cubic.c in the GNU Scientific Library
// (GSL), revision 1.7 of 2003-07-26. For the original source, see
// http://www.gnu.org/software/gsl/
//
// Brian Gough, the author of that code, has granted the
// permission to use it in GNU Classpath under the GNU Classpath
// license, and has assigned the copyright to the Free Software
// Foundation.
//
// The Java implementation is very similar to the GSL code, but
// not a strict one-to-one copy. For example, GSL would sort the
// result.
double a;
double b;
double c;
double q;
double r;
double Q;
double R;
double c3;
double Q3;
double R2;
double CR2;
double CQ3;
// If the cubic coefficient is zero, we have a quadratic equation.
c3 = eqn[3];
if (c3 == 0)
return QuadCurve2D.solveQuadratic(eqn, res);
// Divide the equation by the cubic coefficient.
c = eqn[0] / c3;
b = eqn[1] / c3;
a = eqn[2] / c3;
// We now need to solve x^3 + ax^2 + bx + c = 0.
q = a * a - 3 * b;
r = 2 * a * a * a - 9 * a * b + 27 * c;
Q = q / 9;
R = r / 54;
Q3 = Q * Q * Q;
R2 = R * R;
CR2 = 729 * r * r;
CQ3 = 2916 * q * q * q;
if (R == 0 && Q == 0)
{
// The GNU Scientific Library would return three identical
// solutions in this case.
res[0] = -a / 3;
return 1;
}
if (CR2 == CQ3)
{
/* this test is actually R2 == Q3, written in a form suitable
for exact computation with integers */
/* Due to finite precision some double roots may be missed, and
considered to be a pair of complex roots z = x +/- epsilon i
close to the real axis. */
double sqrtQ = Math.sqrt(Q);
if (R > 0)
{
res[0] = -2 * sqrtQ - a / 3;
res[1] = sqrtQ - a / 3;
}
else
{
res[0] = -sqrtQ - a / 3;
res[1] = 2 * sqrtQ - a / 3;
}
return 2;
}
if (CR2 < CQ3) /* equivalent to R2 < Q3 */
{
double sqrtQ = Math.sqrt(Q);
double sqrtQ3 = sqrtQ * sqrtQ * sqrtQ;
double theta = Math.acos(R / sqrtQ3);
double norm = -2 * sqrtQ;
res[0] = norm * Math.cos(theta / 3) - a / 3;
res[1] = norm * Math.cos((theta + 2.0 * Math.PI) / 3) - a / 3;
res[2] = norm * Math.cos((theta - 2.0 * Math.PI) / 3) - a / 3;
// The GNU Scientific Library sorts the results. We don't.
return 3;
}
double sgnR = (R >= 0 ? 1 : -1);
double A = -sgnR * Math.pow(Math.abs(R) + Math.sqrt(R2 - Q3), 1.0 / 3.0);
double B = Q / A;
res[0] = A + B - a / 3;
return 1;
}
/**
* Determines whether a position lies inside the area bounded
* by the curve and the straight line connecting its end points.
*
*
*
*
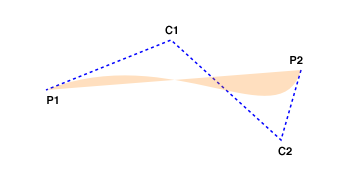
The above drawing illustrates in which area points are
* considered “inside” a CubicCurve2D.
*/
public boolean contains(double x, double y)
{
if (! getBounds2D().contains(x, y))
return false;
return ((getAxisIntersections(x, y, true, BIG_VALUE) & 1) != 0);
}
/**
* Determines whether a point lies inside the area bounded
* by the curve and the straight line connecting its end points.
*
*
*
*
The above drawing illustrates in which area points are
* considered “inside” a CubicCurve2D.
*/
public boolean contains(Point2D p)
{
return contains(p.getX(), p.getY());
}
/**
* Determines whether any part of a rectangle is inside the area bounded
* by the curve and the straight line connecting its end points.
*
*
*
*
The above drawing illustrates in which area points are
* considered “inside” in a CubicCurve2D.
* @see #contains(double, double)
*/
public boolean intersects(double x, double y, double w, double h)
{
if (! getBounds2D().contains(x, y, w, h))
return false;
/* Does any edge intersect? */
if (getAxisIntersections(x, y, true, w) != 0 /* top */
|| getAxisIntersections(x, y + h, true, w) != 0 /* bottom */
|| getAxisIntersections(x + w, y, false, h) != 0 /* right */
|| getAxisIntersections(x, y, false, h) != 0) /* left */
return true;
/* No intersections, is any point inside? */
if ((getAxisIntersections(x, y, true, BIG_VALUE) & 1) != 0)
return true;
return false;
}
/**
* Determines whether any part of a Rectangle2D is inside the area bounded
* by the curve and the straight line connecting its end points.
* @see #intersects(double, double, double, double)
*/
public boolean intersects(Rectangle2D r)
{
return intersects(r.getX(), r.getY(), r.getWidth(), r.getHeight());
}
/**
* Determine whether a rectangle is entirely inside the area that is bounded
* by the curve and the straight line connecting its end points.
*
*
*
*
The above drawing illustrates in which area points are
* considered “inside” a CubicCurve2D.
* @see #contains(double, double)
*/
public boolean contains(double x, double y, double w, double h)
{
if (! getBounds2D().intersects(x, y, w, h))
return false;
/* Does any edge intersect? */
if (getAxisIntersections(x, y, true, w) != 0 /* top */
|| getAxisIntersections(x, y + h, true, w) != 0 /* bottom */
|| getAxisIntersections(x + w, y, false, h) != 0 /* right */
|| getAxisIntersections(x, y, false, h) != 0) /* left */
return false;
/* No intersections, is any point inside? */
if ((getAxisIntersections(x, y, true, BIG_VALUE) & 1) != 0)
return true;
return false;
}
/**
* Determine whether a Rectangle2D is entirely inside the area that is
* bounded by the curve and the straight line connecting its end points.
*
*
*
*
The above drawing illustrates in which area points are
* considered “inside” a CubicCurve2D.
* @see #contains(double, double)
*/
public boolean contains(Rectangle2D r)
{
return contains(r.getX(), r.getY(), r.getWidth(), r.getHeight());
}
/**
* Determines the smallest rectangle that encloses the
* curve’s start, end and control points.
*/
public Rectangle getBounds()
{
return getBounds2D().getBounds();
}
public PathIterator getPathIterator(final AffineTransform at)
{
return new PathIterator()
{
/** Current coordinate. */
private int current = 0;
public int getWindingRule()
{
return WIND_NON_ZERO;
}
public boolean isDone()
{
return current >= 2;
}
public void next()
{
current++;
}
public int currentSegment(float[] coords)
{
int result;
switch (current)
{
case 0:
coords[0] = (float) getX1();
coords[1] = (float) getY1();
result = SEG_MOVETO;
break;
case 1:
coords[0] = (float) getCtrlX1();
coords[1] = (float) getCtrlY1();
coords[2] = (float) getCtrlX2();
coords[3] = (float) getCtrlY2();
coords[4] = (float) getX2();
coords[5] = (float) getY2();
result = SEG_CUBICTO;
break;
default:
throw new NoSuchElementException("cubic iterator out of bounds");
}
if (at != null)
at.transform(coords, 0, coords, 0, 3);
return result;
}
public int currentSegment(double[] coords)
{
int result;
switch (current)
{
case 0:
coords[0] = getX1();
coords[1] = getY1();
result = SEG_MOVETO;
break;
case 1:
coords[0] = getCtrlX1();
coords[1] = getCtrlY1();
coords[2] = getCtrlX2();
coords[3] = getCtrlY2();
coords[4] = getX2();
coords[5] = getY2();
result = SEG_CUBICTO;
break;
default:
throw new NoSuchElementException("cubic iterator out of bounds");
}
if (at != null)
at.transform(coords, 0, coords, 0, 3);
return result;
}
};
}
public PathIterator getPathIterator(AffineTransform at, double flatness)
{
return new FlatteningPathIterator(getPathIterator(at), flatness);
}
/**
* Create a new curve with the same contents as this one.
*
* @return the clone.
*/
public Object clone()
{
try
{
return super.clone();
}
catch (CloneNotSupportedException e)
{
throw (Error) new InternalError().initCause(e); // Impossible
}
}
/**
* Helper method used by contains() and intersects() methods, that
* returns the number of curve/line intersections on a given axis
* extending from a certain point.
*
* @param x x coordinate of the origin point
* @param y y coordinate of the origin point
* @param useYaxis axis used, if true the positive Y axis is used,
* false uses the positive X axis.
*
* This is an implementation of the line-crossings algorithm,
* Detailed in an article on Eric Haines' page:
* http://www.acm.org/tog/editors/erich/ptinpoly/
*
* A special-case not adressed in this code is self-intersections
* of the curve, e.g. if the axis intersects the self-itersection,
* the degenerate roots of the polynomial will erroneously count as
* a single intersection of the curve, and not two.
*/
private int getAxisIntersections(double x, double y, boolean useYaxis,
double distance)
{
int nCrossings = 0;
double a0;
double a1;
double a2;
double a3;
double b0;
double b1;
double b2;
double b3;
double[] r = new double[4];
int nRoots;
a0 = a3 = 0.0;
if (useYaxis)
{
a0 = getY1() - y;
a1 = getCtrlY1() - y;
a2 = getCtrlY2() - y;
a3 = getY2() - y;
b0 = getX1() - x;
b1 = getCtrlX1() - x;
b2 = getCtrlX2() - x;
b3 = getX2() - x;
}
else
{
a0 = getX1() - x;
a1 = getCtrlX1() - x;
a2 = getCtrlX2() - x;
a3 = getX2() - x;
b0 = getY1() - y;
b1 = getCtrlY1() - y;
b2 = getCtrlY2() - y;
b3 = getY2() - y;
}
/* If the axis intersects a start/endpoint, shift it up by some small
amount to guarantee the line is 'inside'
If this is not done, bad behaviour may result for points on that axis.*/
if (a0 == 0.0 || a3 == 0.0)
{
double small = getFlatness() * EPSILON;
if (a0 == 0.0)
a0 -= small;
if (a3 == 0.0)
a3 -= small;
}
if (useYaxis)
{
if (Line2D.linesIntersect(b0, a0, b3, a3, EPSILON, 0.0, distance, 0.0))
nCrossings++;
}
else
{
if (Line2D.linesIntersect(a0, b0, a3, b3, 0.0, EPSILON, 0.0, distance))
nCrossings++;
}
r[0] = a0;
r[1] = 3 * (a1 - a0);
r[2] = 3 * (a2 + a0 - 2 * a1);
r[3] = a3 - 3 * a2 + 3 * a1 - a0;
if ((nRoots = solveCubic(r)) != 0)
for (int i = 0; i < nRoots; i++)
{
double t = r[i];
if (t >= 0.0 && t <= 1.0)
{
double crossing = -(t * t * t) * (b0 - 3 * b1 + 3 * b2 - b3)
+ 3 * t * t * (b0 - 2 * b1 + b2)
+ 3 * t * (b1 - b0) + b0;
if (crossing > 0.0 && crossing <= distance)
nCrossings++;
}
}
return (nCrossings);
}
/**
* A two-dimensional curve that is parameterized with a cubic
* function and stores coordinate values in double-precision
* floating-point format.
*
* @see CubicCurve2D.Float
*
* @author Eric Blake (ebb9@email.byu.edu)
* @author Sascha Brawer (brawer@dandelis.ch)
*/
public static class Double extends CubicCurve2D
{
/**
* The x coordinate of the curve’s start point.
*/
public double x1;
/**
* The y coordinate of the curve’s start point.
*/
public double y1;
/**
* The x coordinate of the curve’s first control point.
*/
public double ctrlx1;
/**
* The y coordinate of the curve’s first control point.
*/
public double ctrly1;
/**
* The x coordinate of the curve’s second control point.
*/
public double ctrlx2;
/**
* The y coordinate of the curve’s second control point.
*/
public double ctrly2;
/**
* The x coordinate of the curve’s end point.
*/
public double x2;
/**
* The y coordinate of the curve’s end point.
*/
public double y2;
/**
* Constructs a new CubicCurve2D that stores its coordinate values
* in double-precision floating-point format. All points are
* initially at position (0, 0).
*/
public Double()
{
}
/**
* Constructs a new CubicCurve2D that stores its coordinate values
* in double-precision floating-point format, specifying the
* initial position of each point.
*
*
*
* @param x1 the x coordinate of the curve’s start
* point.
*
* @param y1 the y coordinate of the curve’s start
* point.
*
* @param cx1 the x coordinate of the curve’s first
* control point.
*
* @param cy1 the y coordinate of the curve’s first
* control point.
*
* @param cx2 the x coordinate of the curve’s second
* control point.
*
* @param cy2 the y coordinate of the curve’s second
* control point.
*
* @param x2 the x coordinate of the curve’s end
* point.
*
* @param y2 the y coordinate of the curve’s end
* point.
*/
public Double(double x1, double y1, double cx1, double cy1, double cx2,
double cy2, double x2, double y2)
{
this.x1 = x1;
this.y1 = y1;
ctrlx1 = cx1;
ctrly1 = cy1;
ctrlx2 = cx2;
ctrly2 = cy2;
this.x2 = x2;
this.y2 = y2;
}
/**
* Returns the x coordinate of the curve’s start
* point.
*/
public double getX1()
{
return x1;
}
/**
* Returns the y coordinate of the curve’s start
* point.
*/
public double getY1()
{
return y1;
}
/**
* Returns the curve’s start point.
*/
public Point2D getP1()
{
return new Point2D.Double(x1, y1);
}
/**
* Returns the x coordinate of the curve’s first
* control point.
*/
public double getCtrlX1()
{
return ctrlx1;
}
/**
* Returns the y coordinate of the curve’s first
* control point.
*/
public double getCtrlY1()
{
return ctrly1;
}
/**
* Returns the curve’s first control point.
*/
public Point2D getCtrlP1()
{
return new Point2D.Double(ctrlx1, ctrly1);
}
/**
* Returns the x coordinate of the curve’s second
* control point.
*/
public double getCtrlX2()
{
return ctrlx2;
}
/**
* Returns the y coordinate of the curve’s second
* control point.
*/
public double getCtrlY2()
{
return ctrly2;
}
/**
* Returns the curve’s second control point.
*/
public Point2D getCtrlP2()
{
return new Point2D.Double(ctrlx2, ctrly2);
}
/**
* Returns the x coordinate of the curve’s end
* point.
*/
public double getX2()
{
return x2;
}
/**
* Returns the y coordinate of the curve’s end
* point.
*/
public double getY2()
{
return y2;
}
/**
* Returns the curve’s end point.
*/
public Point2D getP2()
{
return new Point2D.Double(x2, y2);
}
/**
* Changes the curve geometry, separately specifying each coordinate
* value.
*
*
*
* @param x1 the x coordinate of the curve’s new start
* point.
*
* @param y1 the y coordinate of the curve’s new start
* point.
*
* @param cx1 the x coordinate of the curve’s new
* first control point.
*
* @param cy1 the y coordinate of the curve’s new
* first control point.
*
* @param cx2 the x coordinate of the curve’s new
* second control point.
*
* @param cy2 the y coordinate of the curve’s new
* second control point.
*
* @param x2 the x coordinate of the curve’s new end
* point.
*
* @param y2 the y coordinate of the curve’s new end
* point.
*/
public void setCurve(double x1, double y1, double cx1, double cy1,
double cx2, double cy2, double x2, double y2)
{
this.x1 = x1;
this.y1 = y1;
ctrlx1 = cx1;
ctrly1 = cy1;
ctrlx2 = cx2;
ctrly2 = cy2;
this.x2 = x2;
this.y2 = y2;
}
/**
* Determines the smallest rectangle that encloses the
* curve’s start, end and control points. As the
* illustration below shows, the invisible control points may cause
* the bounds to be much larger than the area that is actually
* covered by the curve.
*
*
*/
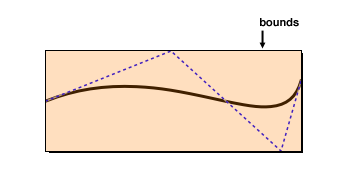public Rectangle2D getBounds2D()
{
double nx1 = Math.min(Math.min(x1, ctrlx1), Math.min(ctrlx2, x2));
double ny1 = Math.min(Math.min(y1, ctrly1), Math.min(ctrly2, y2));
double nx2 = Math.max(Math.max(x1, ctrlx1), Math.max(ctrlx2, x2));
double ny2 = Math.max(Math.max(y1, ctrly1), Math.max(ctrly2, y2));
return new Rectangle2D.Double(nx1, ny1, nx2 - nx1, ny2 - ny1);
}
}
/**
* A two-dimensional curve that is parameterized with a cubic
* function and stores coordinate values in single-precision
* floating-point format.
*
* @see CubicCurve2D.Float
*
* @author Eric Blake (ebb9@email.byu.edu)
* @author Sascha Brawer (brawer@dandelis.ch)
*/
public static class Float extends CubicCurve2D
{
/**
* The x coordinate of the curve’s start point.
*/
public float x1;
/**
* The y coordinate of the curve’s start point.
*/
public float y1;
/**
* The x coordinate of the curve’s first control point.
*/
public float ctrlx1;
/**
* The y coordinate of the curve’s first control point.
*/
public float ctrly1;
/**
* The x coordinate of the curve’s second control point.
*/
public float ctrlx2;
/**
* The y coordinate of the curve’s second control point.
*/
public float ctrly2;
/**
* The x coordinate of the curve’s end point.
*/
public float x2;
/**
* The y coordinate of the curve’s end point.
*/
public float y2;
/**
* Constructs a new CubicCurve2D that stores its coordinate values
* in single-precision floating-point format. All points are
* initially at position (0, 0).
*/
public Float()
{
}
/**
* Constructs a new CubicCurve2D that stores its coordinate values
* in single-precision floating-point format, specifying the
* initial position of each point.
*
*
*
* @param x1 the x coordinate of the curve’s start
* point.
*
* @param y1 the y coordinate of the curve’s start
* point.
*
* @param cx1 the x coordinate of the curve’s first
* control point.
*
* @param cy1 the y coordinate of the curve’s first
* control point.
*
* @param cx2 the x coordinate of the curve’s second
* control point.
*
* @param cy2 the y coordinate of the curve’s second
* control point.
*
* @param x2 the x coordinate of the curve’s end
* point.
*
* @param y2 the y coordinate of the curve’s end
* point.
*/
public Float(float x1, float y1, float cx1, float cy1, float cx2,
float cy2, float x2, float y2)
{
this.x1 = x1;
this.y1 = y1;
ctrlx1 = cx1;
ctrly1 = cy1;
ctrlx2 = cx2;
ctrly2 = cy2;
this.x2 = x2;
this.y2 = y2;
}
/**
* Returns the x coordinate of the curve’s start
* point.
*/
public double getX1()
{
return x1;
}
/**
* Returns the y coordinate of the curve’s start
* point.
*/
public double getY1()
{
return y1;
}
/**
* Returns the curve’s start point.
*/
public Point2D getP1()
{
return new Point2D.Float(x1, y1);
}
/**
* Returns the x coordinate of the curve’s first
* control point.
*/
public double getCtrlX1()
{
return ctrlx1;
}
/**
* Returns the y coordinate of the curve’s first
* control point.
*/
public double getCtrlY1()
{
return ctrly1;
}
/**
* Returns the curve’s first control point.
*/
public Point2D getCtrlP1()
{
return new Point2D.Float(ctrlx1, ctrly1);
}
/**
* Returns the s coordinate of the curve’s second
* control point.
*/
public double getCtrlX2()
{
return ctrlx2;
}
/**
* Returns the y coordinate of the curve’s second
* control point.
*/
public double getCtrlY2()
{
return ctrly2;
}
/**
* Returns the curve’s second control point.
*/
public Point2D getCtrlP2()
{
return new Point2D.Float(ctrlx2, ctrly2);
}
/**
* Returns the x coordinate of the curve’s end
* point.
*/
public double getX2()
{
return x2;
}
/**
* Returns the y coordinate of the curve’s end
* point.
*/
public double getY2()
{
return y2;
}
/**
* Returns the curve’s end point.
*/
public Point2D getP2()
{
return new Point2D.Float(x2, y2);
}
/**
* Changes the curve geometry, separately specifying each coordinate
* value as a double-precision floating-point number.
*
*
*
* @param x1 the x coordinate of the curve’s new start
* point.
*
* @param y1 the y coordinate of the curve’s new start
* point.
*
* @param cx1 the x coordinate of the curve’s new
* first control point.
*
* @param cy1 the y coordinate of the curve’s new
* first control point.
*
* @param cx2 the x coordinate of the curve’s new
* second control point.
*
* @param cy2 the y coordinate of the curve’s new
* second control point.
*
* @param x2 the x coordinate of the curve’s new end
* point.
*
* @param y2 the y coordinate of the curve’s new end
* point.
*/
public void setCurve(double x1, double y1, double cx1, double cy1,
double cx2, double cy2, double x2, double y2)
{
this.x1 = (float) x1;
this.y1 = (float) y1;
ctrlx1 = (float) cx1;
ctrly1 = (float) cy1;
ctrlx2 = (float) cx2;
ctrly2 = (float) cy2;
this.x2 = (float) x2;
this.y2 = (float) y2;
}
/**
* Changes the curve geometry, separately specifying each coordinate
* value as a single-precision floating-point number.
*
*
*
* @param x1 the x coordinate of the curve’s new start
* point.
*
* @param y1 the y coordinate of the curve’s new start
* point.
*
* @param cx1 the x coordinate of the curve’s new
* first control point.
*
* @param cy1 the y coordinate of the curve’s new
* first control point.
*
* @param cx2 the x coordinate of the curve’s new
* second control point.
*
* @param cy2 the y coordinate of the curve’s new
* second control point.
*
* @param x2 the x coordinate of the curve’s new end
* point.
*
* @param y2 the y coordinate of the curve’s new end
* point.
*/
public void setCurve(float x1, float y1, float cx1, float cy1, float cx2,
float cy2, float x2, float y2)
{
this.x1 = x1;
this.y1 = y1;
ctrlx1 = cx1;
ctrly1 = cy1;
ctrlx2 = cx2;
ctrly2 = cy2;
this.x2 = x2;
this.y2 = y2;
}
/**
* Determines the smallest rectangle that encloses the
* curve’s start, end and control points. As the
* illustration below shows, the invisible control points may cause
* the bounds to be much larger than the area that is actually
* covered by the curve.
*
*
*/
public Rectangle2D getBounds2D()
{
float nx1 = Math.min(Math.min(x1, ctrlx1), Math.min(ctrlx2, x2));
float ny1 = Math.min(Math.min(y1, ctrly1), Math.min(ctrly2, y2));
float nx2 = Math.max(Math.max(x1, ctrlx1), Math.max(ctrlx2, x2));
float ny2 = Math.max(Math.max(y1, ctrly1), Math.max(ctrly2, y2));
return new Rectangle2D.Float(nx1, ny1, nx2 - nx1, ny2 - ny1);
}
}
}