Hash Table Design
Overview
The collision-chaining hash-based container has the following declaration.
template<
typename Key,
typename Mapped,
typename Hash_Fn = std::hash<Key>,
typename Eq_Fn = std::equal_to<Key>,
typename Comb_Hash_Fn = direct_mask_range_hashing<>
typename Resize_Policy = default explained below.
bool Store_Hash = false,
typename Allocator = std::allocator<char> >
class cc_hash_table;
The parameters have the following meaning:
- Key is the key type.
- Mapped is the mapped-policy, and is explained in Tutorial::Associative Containers::Associative Containers Others than Maps.
- Hash_Fn is a key hashing functor.
- Eq_Fn is a key equivalence functor.
- Comb_Hash_Fn is a range-hashing_functor; it describes how to translate hash values into positions within the table. This is described in Hash Policies.
- Resize_Policy describes how a container object should change its internal size. This is described in Resize Policies.
- Store_Hash indicates whether the hash value should be stored with each entry. This is described in Policy Interaction.
- Allocator is an allocator type.
The probing hash-based container has the following declaration.
template<
typename Key,
typename Mapped,
typename Hash_Fn = std::hash<Key>,
typename Eq_Fn = std::equal_to<Key>,
typename Comb_Probe_Fn = direct_mask_range_hashing<>
typename Probe_Fn = default explained below.
typename Resize_Policy = default explained below.
bool Store_Hash = false,
typename Allocator = std::allocator<char> >
class gp_hash_table;
The parameters are identical to those of the collision-chaining container, except for the following.
- Comb_Probe_Fn describes how to transform a probe sequence into a sequence of positions within the table.
- Probe_Fn describes a probe sequence policy.
Some of the default template values depend on the values of other parameters, and are explained in Policy Interaction.
Hash Policies
General Terms
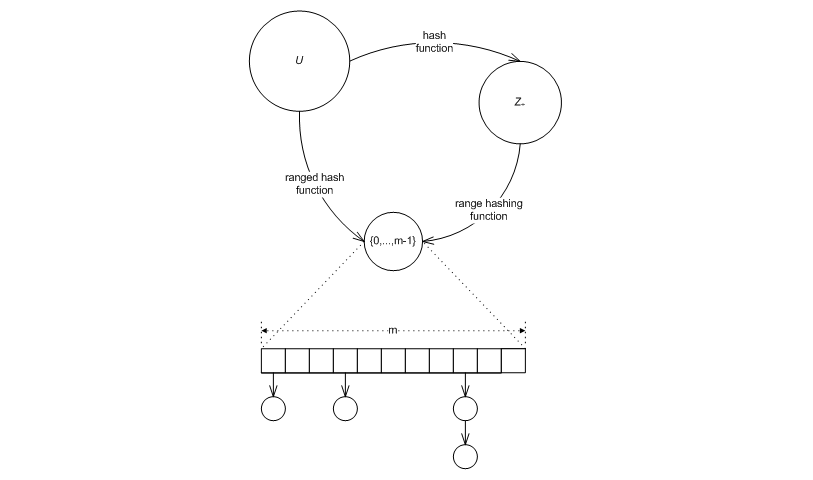
Following is an explanation of some functions which hashing involves. Figure Hash functions, ranged-hash functions, and range-hashing functions) illustrates the discussion.
Hash functions, ranged-hash functions, and range-hashing functions.
Let U be a domain (e.g., the integers, or the strings of 3 characters). A hash-table algorithm needs to map elements of U "uniformly" into the range [0,..., m - 1] (where m is a non-negative integral value, and is, in general, time varying). I.e., the algorithm needs a ranged-hash function
f : U × Z+ → Z+ ,
such that for any u in U ,
0 ≤ f(u, m) ≤ m - 1 ,
and which has "good uniformity" properties [knuth98sorting]. One common solution is to use the composition of the hash function
h : U → Z+ ,
which maps elements of U into the non-negative integrals, and
g : Z+ × Z+ → Z+,
which maps a non-negative hash value, and a non-negative range upper-bound into a non-negative integral in the range between 0 (inclusive) and the range upper bound (exclusive), i.e., for any r in Z+,
0 ≤ g(r, m) ≤ m - 1 .
The resulting ranged-hash function, is
f(u , m) = g(h(u), m) (1) .
From the above, it is obvious that given g and h, f can always be composed (however the converse is not true). The STL's hash-based containers allow specifying a hash function, and use a hard-wired range-hashing function; the ranged-hash function is implicitly composed.
The above describes the case where a key is to be mapped into a single position within a hash table, e.g., in a collision-chaining table. In other cases, a key is to be mapped into a sequence of positions within a table, e.g., in a probing table. Similar terms apply in this case: the table requires a ranged probe function, mapping a key into a sequence of positions withing the table. This is typically achieved by composing a hash function mapping the key into a non-negative integral type, a probe function transforming the hash value into a sequence of hash values, and a range-hashing function transforming the sequence of hash values into a sequence of positions.
Range-Hashing Functions
Some common choices for range-hashing functions are the division, multiplication, and middle-square methods [knuth98sorting], defined as
g(r, m) = r mod m (2) ,
g(r, m) = ⌈ u/v ( a r mod v ) ⌉ ,
and
g(r, m) = ⌈ u/v ( r2 mod v ) ⌉ ,
respectively, for some positive integrals u and v (typically powers of 2), and some a. Each of these range-hashing functions works best for some different setting.
The division method (2) is a very common choice. However, even this single method can be implemented in two very different ways. It is possible to implement (2) using the low level % (modulo) operation (for any m), or the low level & (bit-mask) operation (for the case where m is a power of 2), i.e.,
g(r, m) = r % m (3) ,
and
g(r, m) = r & m - 1, (m = 2k) for some k) (4),
respectively.
The % (modulo) implementation (3) has the advantage that for m a prime far from a power of 2, g(r, m) is affected by all the bits of r (minimizing the chance of collision). It has the disadvantage of using the costly modulo operation. This method is hard-wired into SGI's implementation [sgi_stl].
The & (bit-mask) implementation (4) has the advantage of relying on the fast bit-wise and operation. It has the disadvantage that for g(r, m) is affected only by the low order bits of r. This method is hard-wired into Dinkumware's implementation [dinkumware_stl].
Ranged-Hash Functions
In cases it is beneficial to allow the client to directly specify a ranged-hash hash function. It is true, that the writer of the ranged-hash function cannot rely on the values of m having specific numerical properties suitable for hashing (in the sense used in [knuth98sorting]), since the values of m are determined by a resize policy with possibly orthogonal considerations.
There are two cases where a ranged-hash function can be superior. The firs is when using perfect hashing [knuth98sorting]; the second is when the values of m can be used to estimate the "general" number of distinct values required. This is described in the following.
Let
s = [ s0,..., st - 1]
be a string of t characters, each of which is from domain S. Consider the following ranged-hash function:
f1(s, m) = ∑ i = 0t - 1 si ai mod m (5) ,
where a is some non-negative integral value. This is the standard string-hashing function used in SGI's implementation (with a = 5) [sgi_stl]. Its advantage is that it takes into account all of the characters of the string.
Now assume that s is the string representation of a of a long DNA sequence (and so S = {'A', 'C', 'G', 'T'}). In this case, scanning the entire string might be prohibitively expensive. A possible alternative might be to use only the first k characters of the string, where
|S|k ≥ m ,
i.e., using the hash function
f2(s, m) = ∑ i = 0k - 1 si ai mod m , (6)
requiring scanning over only
k = log4( m )
characters.
Other more elaborate hash-functions might scan k characters starting at a random position (determined at each resize), or scanning k random positions (determined at each resize), i.e., using
f3(s, m) = ∑ i = r0r0 + k - 1 si ai mod m ,
or
f4(s, m) = ∑ i = 0k - 1 sri ari mod m ,
respectively, for r0,..., rk-1 each in the (inclusive) range [0,...,t-1].
It should be noted that the above functions cannot be decomposed as (1) .
Implementation
This sub-subsection describes the implementation of the above in pb_ds. It first explains range-hashing functions in collision-chaining tables, then ranged-hash functions in collision-chaining tables, then probing-based tables, and, finally, lists the relevant classes in pb_ds.
Range-Hashing and Ranged-Hashes in Collision-Chaining Tables
cc_hash_table is parametrized by Hash_Fn and Comb_Hash_Fn, a hash functor and a combining hash functor, respectively.
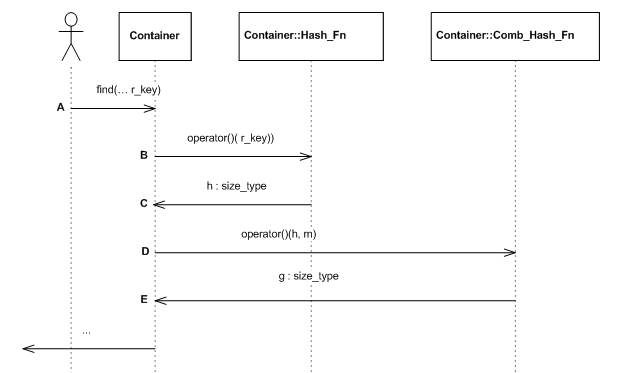
In general, Comb_Hash_Fn is considered a range-hashing functor. cc_hash_table synthesizes a ranged-hash function from Hash_Fn and Comb_Hash_Fn (see (1) above). Figure Insert hash sequence diagram shows an insert sequence diagram for this case. The user inserts an element (point A), the container transforms the key into a non-negative integral using the hash functor (points B and C), and transforms the result into a position using the combining functor (points D and E).
Insert hash sequence diagram.
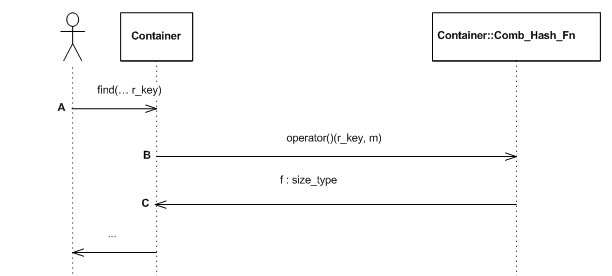
If cc_hash_table's hash-functor, Hash_Fn is instantiated by null_hash_fn (see Interface::Concepts::Null Policy Classes), then Comb_Hash_Fn is taken to be a ranged-hash function. Figure Insert hash sequence diagram with a null hash policy shows an insert sequence diagram. The user inserts an element (point A), the container transforms the key into a position using the combining functor (points B and C).
Insert hash sequence diagram with a null hash policy.
Probing Tables
gp_hash_table is parametrized by Hash_Fn, Probe_Fn, and Comb_Probe_Fn. As before, if Hash_Fn and Probe_Fn are, respectively, null_hash_fn and null_probe_fn, then Comb_Probe_Fn is a ranged-probe functor. Otherwise, Hash_Fn is a hash functor, Probe_Fn is a functor for offsets from a hash value, and Comb_Probe_Fn transforms a probe sequence into a sequence of positions within the table.
Pre-Defined Policies
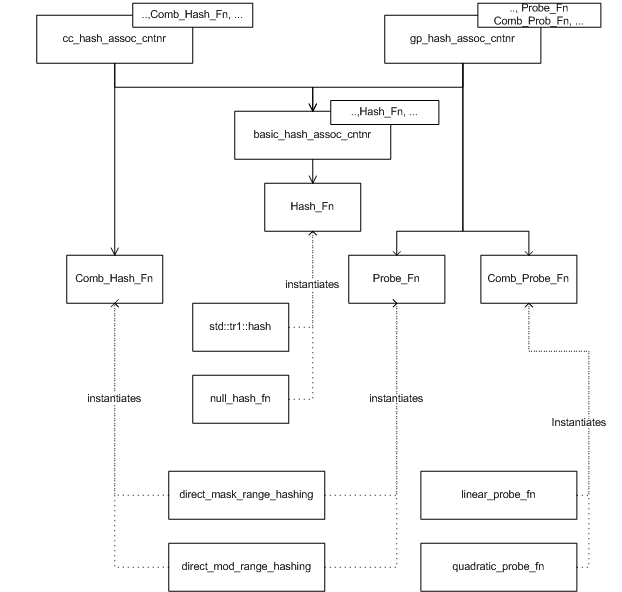
pb_ds contains some pre-defined classes implementing range-hashing and probing functions:
- direct_mask_range_hashing and direct_mod_range_hashing are range-hashing functions based on a bit-mask and a modulo operation, respectively.
- linear_probe_fn, and quadratic_probe_fn are a linear probe and a quadratic probe function, respectively.
Hash policy class diagram.
Resize Policies
General Terms
Hash-tables, as opposed to trees, do not naturally grow or shrink. It is necessary to specify policies to determine how and when a hash table should change its size. Usually, resize policies can be decomposed into orthogonal policies:
- A size policy indicating how a hash table should grow (e.g., it should multiply by powers of 2).
- A trigger policy indicating when a hash table should grow (e.g., a load factor is exceeded).
Size Policies
Size policies determine how a hash table changes size. These policies are simple, and there are relatively few sensible options. An exponential-size policy (with the initial size and growth factors both powers of 2) works well with a mask-based range-hashing function (see Range-Hashing Policies), and is the hard-wired policy used by Dinkumware [dinkumware_stl]. A prime-list based policy works well with a modulo-prime range hashing function (see Range-Hashing Policies), and is the hard-wired policy used by SGI's implementation [sgi_stl].
Trigger Policies
Trigger policies determine when a hash table changes size. Following is a description of two policies: load-check policies, and collision-check policies.
Load-check policies are straightforward. The user specifies two factors, αmin and αmax, and the hash table maintains the invariant that
αmin ≤ (number of stored elements) / (hash-table size) ≤ αmax (1) .
Collision-check policies work in the opposite direction of load-check policies. They focus on keeping the number of collisions moderate and hoping that the size of the table will not grow very large, instead of keeping a moderate load-factor and hoping that the number of collisions will be small. A maximal collision-check policy resizes when the longest probe-sequence grows too large.
Consider Figure Balls and bins. Let the size of the hash table be denoted by m, the length of a probe sequence be denoted by k, and some load factor be denoted by α. We would like to calculate the minimal length of k, such that if there were α m elements in the hash table, a probe sequence of length k would be found with probability at most 1/m.
Balls and bins.
Denote the probability that a probe sequence of length k appears in bin i by pi, the length of the probe sequence of bin i by li, and assume uniform distribution. Then
p1 = (3)
P(l1 ≥ k) =
P(l1 ≥ α ( 1 + k / α - 1 ) ≤ (a)
e ^ ( - ( α ( k / α - 1 )2 ) /2 ) ,
where (a) follows from the Chernoff bound [motwani95random]. To calculate the probability that some bin contains a probe sequence greater than k, we note that the li are negatively-dependent [dubhashi98neg]. Let I(.) denote the indicator function. Then
P ( ∑ i = 1m I(li ≥ k) ≥ 1 ) =
P ( ∑ i = 1m I ( li ≥ k ) ≥ m p1 ( 1 + 1 / (m p1) - 1 ) ) ≤ (a)
e ^ ( ( - m p1 ( 1 / (m p1) - 1 ) 2 ) / 2 ) ,
where (a) follows from the fact that the Chernoff bound can be applied to negatively-dependent variables [dubhashi98neg]. Inserting (2) into (3), and equating with 1/m, we obtain
k ~ √ ( 2 α ln 2 m ln(m) ) ) .
Implementation
This sub-subsection describes the implementation of the above in pb_ds. It first describes resize policies and their decomposition into trigger and size policies, then describes pre-defined classes, and finally discusses controlled access the policies' internals.
Resize Policies and Their Decomposition
Each hash-based container is parametrized by a Resize_Policy parameter; the container derives publicly from Resize_Policy. For example:
cc_hash_table< typename Key, typename Mapped, ... typename Resize_Policy ...> : public Resize_Policy
As a container object is modified, it continuously notifies its Resize_Policy base of internal changes (e.g., collisions encountered and elements being inserted). It queries its Resize_Policy base whether it needs to be resized, and if so, to what size.
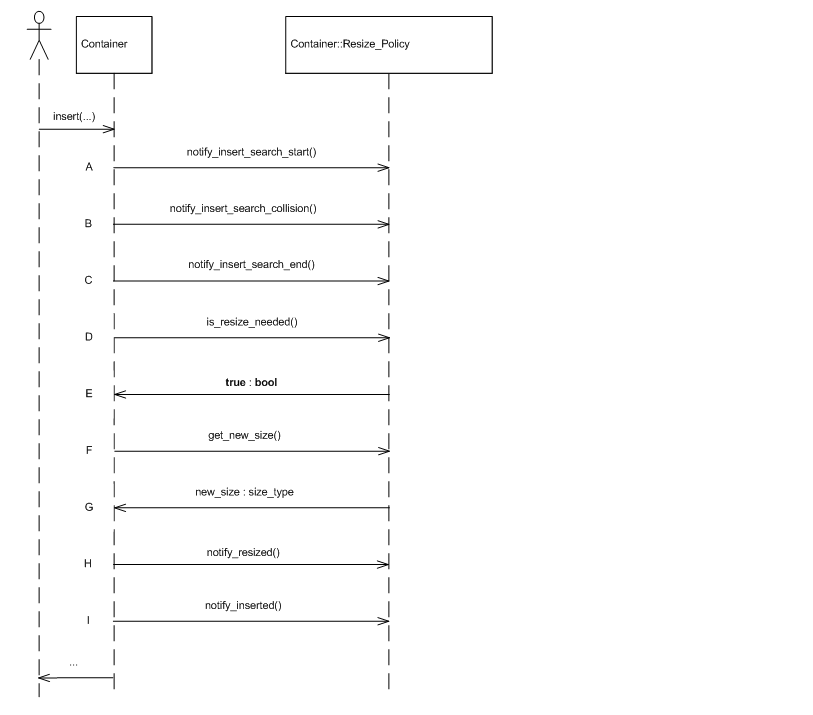
Figure Insert resize sequence diagram shows a (possible) sequence diagram of an insert operation. The user inserts an element; the hash table notifies its resize policy that a search has started (point A); in this case, a single collision is encountered - the table notifies its resize policy of this (point B); the container finally notifies its resize policy that the search has ended (point C); it then queries its resize policy whether a resize is needed, and if so, what is the new size (points D to G); following the resize, it notifies the policy that a resize has completed (point H); finally, the element is inserted, and the policy notified (point I).
Insert resize sequence diagram.
In practice, a resize policy can be usually orthogonally decomposed to a size policy and a trigger policy. Consequently, the library contains a single class for instantiating a resize policy: hash_standard_resize_policy is parametrized by Size_Policy and Trigger_Policy, derives publicly from both, and acts as a standard delegate [gamma95designpatterns] to these policies.
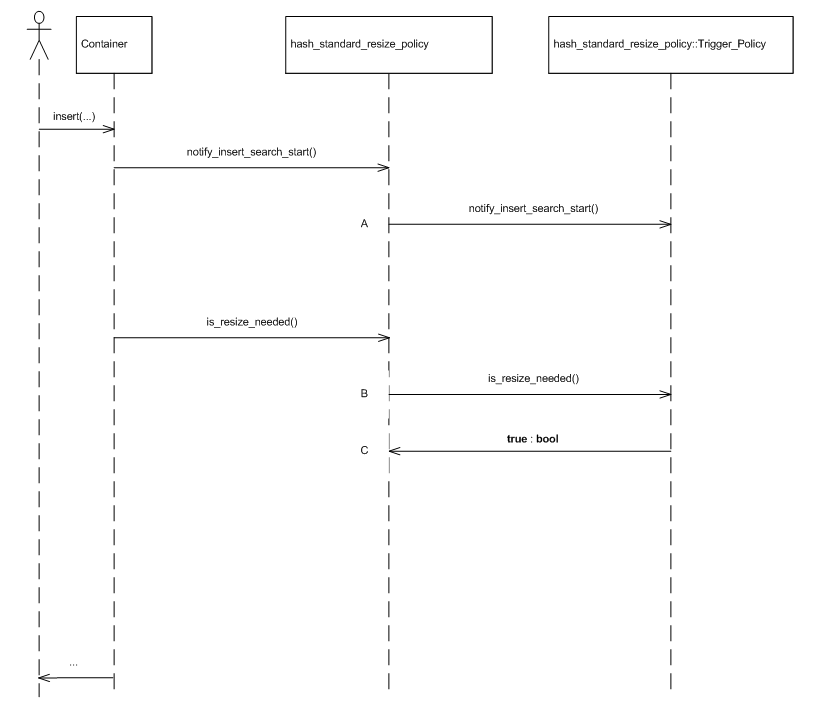
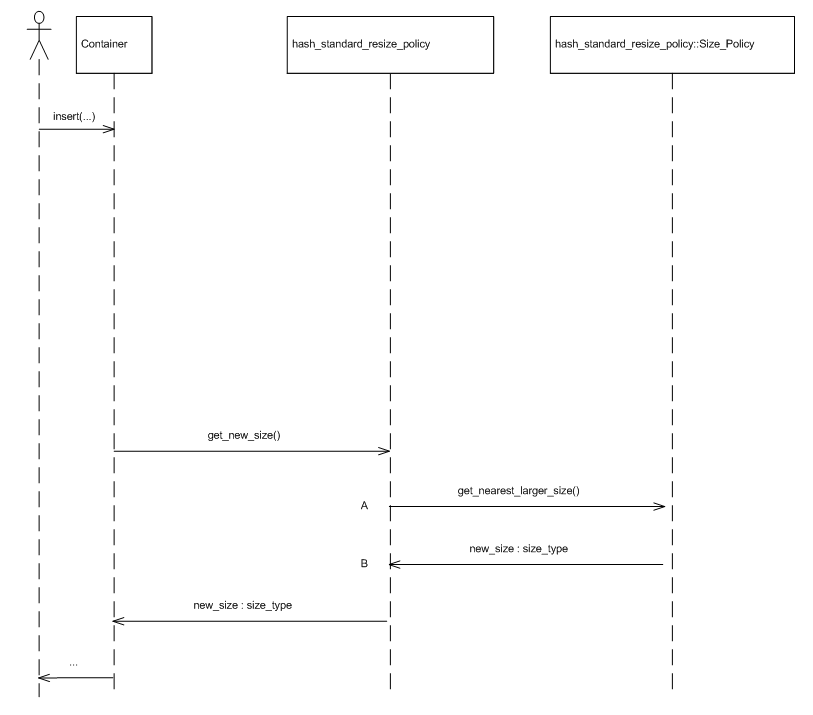
Figures Standard resize policy trigger sequence diagram and Standard resize policy size sequence diagram show sequence diagrams illustrating the interaction between the standard resize policy and its trigger and size policies, respectively.
Standard resize policy trigger sequence diagram.
Standard resize policy size sequence diagram.
Pre-Defined Policies
The library includes the following instantiations of size and trigger policies:
- hash_load_check_resize_trigger implements a load check trigger policy.
- cc_hash_max_collision_check_resize_trigger implements a collision check trigger policy.
- hash_exponential_size_policy implements an exponential-size policy (which should be used with mask range hashing).
- hash_prime_size_policy implementing a size policy based on a sequence of primes [sgi_stl] (which should be used with mod range hashing
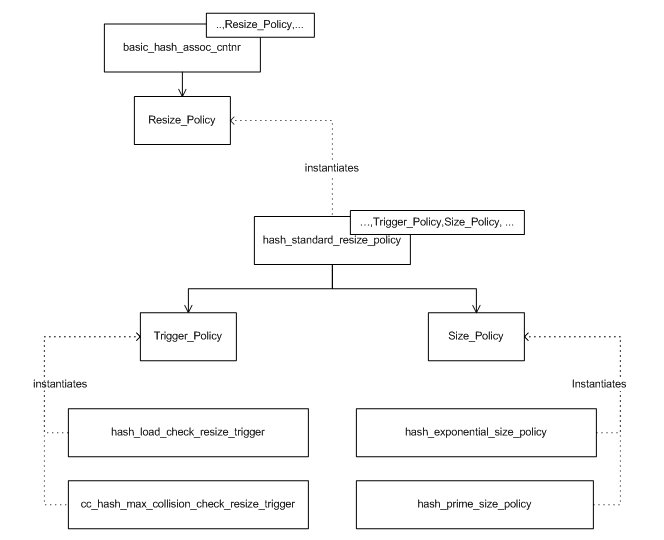
Figure Resize policy class diagram gives an overall picture of the resize-related classes. basic_hash_table is parametrized by Resize_Policy, which it subclasses publicly. This class is currently instantiated only by hash_standard_resize_policy. hash_standard_resize_policy itself is parametrized by Trigger_Policy and Size_Policy. Currently, Trigger_Policy is instantiated by hash_load_check_resize_trigger, or cc_hash_max_collision_check_resize_trigger; Size_Policy is instantiated by hash_exponential_size_policy, or hash_prime_size_policy.
Resize policy class diagram.
Controlled Access to Policies' Internals
There are cases where (controlled) access to resize policies' internals is beneficial. E.g., it is sometimes useful to query a hash-table for the table's actual size (as opposed to its size() - the number of values it currently holds); it is sometimes useful to set a table's initial size, externally resize it, or change load factors.
Clearly, supporting such methods both decreases the encapsulation of hash-based containers, and increases the diversity between different associative-containers' interfaces. Conversely, omitting such methods can decrease containers' flexibility.
In order to avoid, to the extent possible, the above conflict, the hash-based containers themselves do not address any of these questions; this is deferred to the resize policies, which are easier to change or replace. Thus, for example, neither cc_hash_table nor gp_hash_table contain methods for querying the actual size of the table; this is deferred to hash_standard_resize_policy.
Furthermore, the policies themselves are parametrized by template arguments that determine the methods they support ([alexandrescu01modern] shows techniques for doing so). hash_standard_resize_policy is parametrized by External_Size_Access that determines whether it supports methods for querying the actual size of the table or resizing it. hash_load_check_resize_trigger is parametrized by External_Load_Access that determines whether it supports methods for querying or modifying the loads. cc_hash_max_collision_check_resize_trigger is parametrized by External_Load_Access that determines whether it supports methods for querying the load.
Some operations, for example, resizing a container at run time, or changing the load factors of a load-check trigger policy, require the container itself to resize. As mentioned above, the hash-based containers themselves do not contain these types of methods, only their resize policies. Consequently, there must be some mechanism for a resize policy to manipulate the hash-based container. As the hash-based container is a subclass of the resize policy, this is done through virtual methods. Each hash-based container has a private virtual method:
virtual void
do_resize
(size_type new_size);
which resizes the container. Implementations of Resize_Policy can export public methods for resizing the container externally; these methods internally call do_resize to resize the table.
Policy Interaction
Hash-tables are unfortunately especially susceptible to choice of policies. One of the more complicated aspects of this is that poor combinations of good policies can form a poor container. Following are some considerations.
Probe Policies, Size Policies, and Trigger Policies
Some combinations do not work well for probing containers. For example, combining a quadratic probe policy with an exponential size policy can yield a poor container: when an element is inserted, a trigger policy might decide that there is no need to resize, as the table still contains unused entries; the probe sequence, however, might never reach any of the unused entries.
Unfortunately, pb_ds cannot detect such problems at compilation (they are halting reducible). It therefore defines an exception class insert_error to throw an exception in this case.
Hash Policies and Trigger Policies
Some trigger policies are especially susceptible to poor hash functions. Suppose, as an extreme case, that the hash function transforms each key to the same hash value. After some inserts, a collision detecting policy will always indicate that the container needs to grow.
The library, therefore, by design, limits each operation to one resize. For each insert, for example, it queries only once whether a resize is needed.
Equivalence Functors, Storing Hash Values, and Hash Functions
cc_hash_table and gp_hash_table are parametrized by an equivalence functor and by a Store_Hash parameter. If the latter parameter is true, then the container stores with each entry a hash value, and uses this value in case of collisions to determine whether to apply a hash value. This can lower the cost of collision for some types, but increase the cost of collisions for other types.
If a ranged-hash function or ranged probe function is directly supplied, however, then it makes no sense to store the hash value with each entry. pb_ds's container will fail at compilation, by design, if this is attempted.
Size Policies and Load-Check Trigger Policies
Assume a size policy issues an increasing sequence of sizes a, a q, a q1, a q2, ... For example, an exponential size policy might issue the sequence of sizes 8, 16, 32, 64, ...
If a load-check trigger policy is used, with loads αmin and αmax, respectively, then it is a good idea to have:
- αmax ~ 1 / q
- αmin < 1 / (2 q)
This will ensure that the amortized hash cost of each modifying operation is at most approximately 3.
αmin ~ αmax is, in any case, a bad choice, and αmin > αmax is horrendous.