Trie Design
Overview
The trie-based container has the following declaration:
template<
typename Key,
typename Mapped,
typename Cmp_Fn = std::less<Key>,
typename Tag = pat_trie_tag,
template<
typename Const_Node_Iterator,
typename Node_Iterator,
typename E_Access_Traits_,
typename Allocator_>
class Node_Update = null_trie_node_update,
typename Allocator = std::allocator<char> >
class trie;
The parameters have the following meaning:
- Key is the key type.
- Mapped is the mapped-policy, and is explained in Tutorial::Associative Containers::Associative Containers Others than Maps.
- E_Access_Traits is described in Element-Access Traits.
- Tag specifies which underlying data structure to use, and is described shortly.
- Node_Update is a policy for updating node invariants. This is described in Node Invariants.
- Allocator is an allocator type.
The Tag parameter specifies which underlying data structure to use. Instantiating it by pat_trie_tag, specifies an underlying PATRICIA trie (explained shortly); any other tag is currently illegal.
Following is a description of a (PATRICIA) trie (pb_ds follows specifically [okasaki98mereable] and [filliatre2000ptset]).
A (PATRICIA) trie is similar to a tree, but with the following differences:
- It explicitly views keys as a sequence of elements. E.g., a trie can view a string as a sequence of characters; a trie can view a number as a sequence of bits.
- It is not (necessarily) binary. Each node has fan-out n + 1, where n is the number of distinct elements.
- It stores values only at leaf nodes.
- Internal nodes have the properties that A) each has at least two children, and B) each shares the same prefix with any of its descendant.
Element-Access Traits shows an example of such a trie.
A (PATRICIA) trie has some useful properties:
- It can be configured to use large node fan-out, giving it very efficient find performance (albeit at insertion complexity and size).
- It works well for common-prefix keys.
- It can support efficiently queries such as which keys match a certain prefix. This is sometimes useful in file systems and routers.
(We would like to thank Matt Austern for the suggestion to include tries.)
Element-Access Traits
A trie inherently views its keys as sequences of elements. For example, a trie can view a string as a sequence of characters. A trie needs to map each of n elements to a number in {0, n - 1}. For example, a trie can map a character c to static_cast<size_t>(c).
Seemingly, then, a trie can assume that its keys support (const) iterators, and that the value_type of this iterator can be cast to a size_t. There are several reasons, though, to decouple the mechanism by which the trie accesses its keys' elements from the trie:
- In some cases, the numerical value of an element is inappropriate. Consider a trie storing DNA strings. It is logical to use a trie with a fan-out of 5 = 1 + |{'A', 'C', 'G', 'T'}|. This requires mapping 'T' to 3, though.
- In some cases the keys' iterators are different than what is needed. For example, a trie can be used to search for common suffixes, by using strings' reverse_iterator. As another example, a trie mapping UNICODE strings would have a huge fan-out if each node would branch on a UNICODE character; instead, one can define an iterator iterating over 8-bit (or less) groups.
trie is, consequently, parametrized by E_Access_Traits - traits which instruct how to access sequences' elements. string_trie_e_access_traits is a traits class for strings. Each such traits define some types, e.g.,
typename E_Access_Traits::const_iterator
is a const iterator iterating over a key's elements. The traits class must also define methods for obtaining an iterator to the first and last element of a key.
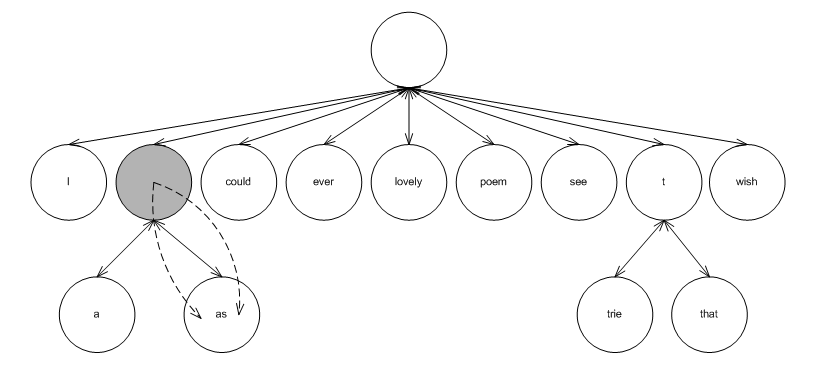
Figure A PATRICIA trie shows a (PATRICIA) trie resulting from inserting the words: "I wish that I could ever see a poem lovely as a trie" (which, unfortunately, does not rhyme).
The leaf nodes contain values; each internal node contains two typename E_Access_Traits::const_iterator objects, indicating the maximal common prefix of all keys in the sub-tree. For example, the shaded internal node roots a sub-tree with leafs "a" and "as". The maximal common prefix is "a". The internal node contains, consequently, to const iterators, one pointing to 'a', and the other to 's'.
A PATRICIA trie.
Node Invariants
Trie-based containers support node invariants, as do tree-based containers (see Tree-Based Containers::Node Invariants). There are two minor differences, though, which, unfortunately, thwart sharing them sharing the same node-updating policies:
- A trie's Node_Update template-template parameter is parametrized by E_Access_Traits, while a tree's Node_Update template-template parameter is parametrized by Cmp_Fn.
- Tree-based containers store values in all nodes, while trie-based containers (at least in this implementation) store values in leafs.
Figure A trie and its update policy shows the scheme, as well as some predefined policies (which are explained below).
A trie and its update policy.
pb_ds offers the following pre-defined trie node updating policies:
- trie_order_statistics_node_update supports order statistics.
- trie_prefix_search_node_update supports searching for ranges that match a given prefix. See trie_prefix_search.cc.
- null_trie_node_update is the null node updater.
Additional Methods
Trie-based containers support split and join methods; the rationale is equal to that of tree-based containers supporting these methods (see Tree-Based Containers::Additional Methods).