Motivation

Many fine associative-container libraries were already written, most notably, the STL's associative containers. Why then write another library? This section shows some possible advantages of this library, when considering the challenges in Introduction. Many of these points stem from the fact that the STL introduced associative-containers in a two-step process (first standardizing tree-based containers, only then adding hash-based containers, which are fundamentally different), did not standardize priority queues as containers, and (in our opinion) overloads the iterator concept.

Associative Containers

More Configuration Choices

Associative containers require a relatively large number of policies to function efficiently in various settings. In some cases this is needed for making their common operations more efficient, and in other cases this allows them to support a larger set of operations

Hash-based containers, for example, support look-up and insertion methods (e.g., find and insert). In order to locate elements quickly, they are supplied a hash functor, which instruct how to transform a key object into some size type; e.g., a hash functor might transform "hello" into 1123002298. A hash table, though, requires transforming each key object into some size-type type in some specific domain; e.g., a hash table with a 128-long table might transform "hello" into position 63. The policy by which the hash value is transformed into a position within the table can dramatically affect performance (see Design::Associative Containers::Hash-Based Containers::Hash Policies). Hash-based containers also do not resize naturally (as opposed to tree-based containers, for example). The appropriate resize policy is unfortunately intertwined with the policy that transforms hash value into a position within the table (see Design::Associative Containers::Hash-Based Containers::Resize Policies).
Associative-Container Performance Tests::Hash-Based Containers quantifies some of these points.
Tree-based containers, for example, also support look-up and insertion methods, and are primarily useful when maintaining order between elements is important. In some cases, though, one can utilize their balancing algorithms for completely different purposes.
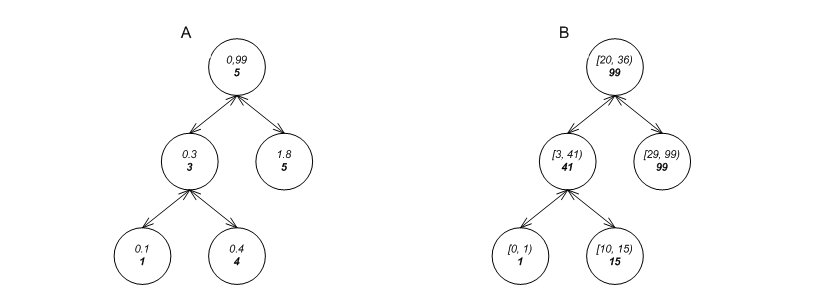
Figure Metadata for order-statistics and interval intersections-A, for example, shows a tree whose each node contains two entries: a floating-point key, and some size-type metadata (in bold beneath it) that is the number of nodes in the sub-tree. (E.g., the root has key 0.99, and has 5 nodes (including itself) in its sub-tree.) A container based on this data structure can obviously answer efficiently whether 0.3 is in the container object, but it can also answer what is the order of 0.3 among all those in the container object [clrs2001] (see Associative Container Examples::Tree-Like-Based Containers (Trees and Tries)).

As another example, Figure Metadata for order-statistics and interval intersections-B shows a tree whose each node contains two entries: a half-open geometric line interval, and a number metadata (in bold beneath it) that is the largest endpoint of all intervals in its sub-tree. (E.g., the root describes the interval [20, 36), and the largest endpoint in its sub-tree is 99.) A container based on this data structure can obviously answer efficiently whether [3, 41) is in the container object, but it can also answer efficiently whether the container object has intervals that intersect [3, 41) (see Associative Container Examples::Tree-Like-Based Containers (Trees and Tries)). These types of queries are very useful in geometric algorithms and lease-management algorithms.

It is important to note, however, that as the trees are modified, their internal structure changes. To maintain these invariants, one must supply some policy that is aware of these changes (see Design::Associative Containers::Tree-Based Containers::Node Invariants); without this, it would be better to use a linked list (in itself very efficient for these purposes).

Associative-Container Performance Tests::Tree-Like-Based Containers quantifies some of these points.

Metadata for order-statistics and interval intersections.

More Data Structures and Traits

The STL contains associative containers based on red-black trees and collision-chaining hash tables. These are obviously very useful, but they are not ideal for all types of settings.

Figure Different underlying data structures shows different underlying data structures (the ones currently supported in pb_ds). A shows a collision-chaining hash-table, B shows a probing hash-table, C shows a red-black tree, D shows a splay tree, E shows a tree based on an ordered vector(implicit in the order of the elements), F shows a PATRICIA trie, and G shows a list-based container with update policies.

Each of these data structures has some performance benefits, in terms of speed, size or both (see Associative-Container Performance Tests and Associative-Container Performance Tests::Observations::Underlying Data-Structure Families). For now, though, note that e.g., vector-based trees and probing hash tables manipulate memory more efficiently than red-black trees and collision-chaining hash tables, and that list-based associative containers are very useful for constructing "multimaps" (see Alternative to Multiple Equivalent Keys, Associative Container Performance Tests::Multimaps, and Associative Container Performance Tests::Observations::Mapping-Semantics Considerations).

Different underlying data structures.

Now consider a function manipulating a generic associative container, e.g.,

template<
    class Cntnr>
int 
    some_op_sequence
    (Cntnr &r_cnt)
{
    ...
}

Ideally, the underlying data structure of Cntnr would not affect what can be done with r_cnt. Unfortunately, this is not the case.

For example, if Cntnr is std::map, then the function can use std::for_each(r_cnt.find(foo), r_cnt.find(bar), foobar) in order to apply foobar to all elements between foo and bar. If Cntnr is a hash-based container, then this call's results are undefined.

Also, if Cntnr is tree-based, the type and object of the comparison functor can be accessed. If Cntnr is hash based, these queries are nonsensical.

There are various other differences based on the container's underlying data structure. For one, they can be constructed by, and queried for, different policies. Furthermore:

Containers based on C, D, E and F store elements in a meaningful order; the others store elements in a meaningless (and probably time-varying) order. By implication, only containers based on C, D, E and F can support erase operations taking an iterator and returning an iterator to the following element without performance loss (see Slightly Different Methods::Methods Related to Erase).
Containers based on C, D, E, and F can be split and joined efficiently, while the others cannot. Containers based on C and D, furthermore, can guarantee that this is exception-free; containers based on E cannot guarantee this.
Containers based on all but E can guarantee that erasing an element is exception free; containers based on E cannot guarantee this. Containers based on all but B and E can guarantee that modifying an object of their type does not invalidate iterators or references to their elements, while containers based on B and E cannot. Containers based on C, D, and E can furthermore make a stronger guarantee, namely that modifying an object of their type does not affect the order of iterators.

A unified tag and traits system (as used for the STL's iterators, for example) can ease generic manipulation of associative containers based on different underlying data structures (see Tutorial::Associative Containers::Determining Containers' Attributes and Design::Associative Containers::Data-Structure Genericity::Data-Structure Tags and Traits).

Differentiating between Iterator Types

Iterators are centric to the STL's design, because of the container/algorithm/iterator decomposition that allows an algorithm to operate on a range through iterators of some sequence (e.g., one originating from a container). Iterators, then, are useful because they allow going over a sequence. The STL also uses iterators for accessing a specific element - e.g., when an associative container returns one through find. The STL, however, consistently uses the same types of iterators for both purposes: going over a range, and accessing a specific found element. Before the introduction of hash-based containers to the STL, this made sense (with the exception of priority queues, which are discussed in Priority Queues).

Using the STL's associative containers together with non-order-preserving associative containers (and also because of priority-queues container), there is a possible need for different types of iterators for self-organizing containers - the iterator concept seems overloaded to mean two different things (in some cases). The following subsections explain this; Tutorial::Associative Containers::Point-Type and Range-Type Methods explains an alternative design which does not complicate the use of order-preserving containers, but is better for unordered containers; Design::Associative Containers::Data-Structure Genericity::Point-Type and Range-Type Methods explains the design further.

Using Point-Type Iterators for Range-Type Operations

Suppose cntnr is some associative container, and say c is an object of type cntnr. Then what will be the outcome of

std::for_each(c.find(1), c.find(5), foo);

If cntnr is a tree-based container object, then an in-order walk will apply foo to the relevant elements, e.g., as in Figure Range iteration in different data structures -A. If c is a hash-based container, then the order of elements between any two elements is undefined (and probably time-varying); there is no guarantee that the elements traversed will coincide with the logical elements between 1 and 5, e.g., as in Figure Range iteration in different data structures-B.

Range iteration in different data structures.

In our opinion, this problem is not caused just because red-black trees are order preserving while collision-chaining hash tables are (generally) not - it is more fundamental. Most of the STL's containers order sequences in a well-defined manner that is determined by their interface: calling insert on a tree-based container modifies its sequence in a predictable way, as does calling push_back on a list or a vector. Conversely, collision-chaining hash tables, probing hash tables, priority queues, and list-based containers (which are very useful for "multimaps") are self-organizing data structures; the effect of each operation modifies their sequences in a manner that is (practically) determined by their implementation.

Consequently, applying an algorithm to a sequence obtained from most containers may or may not make sense, but applying it to a sub-sequence of a self-organizing container does not.

The Cost of Enabling Range Capabilities to Point-Type Iterators

Suppose c is some collision-chaining hash-based container object, and one calls c.find(3). Then what composes the returned iterator?

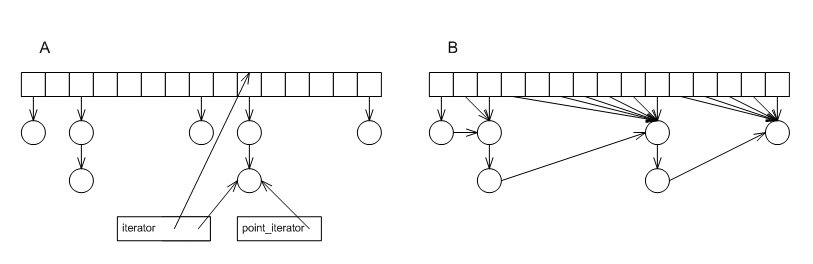
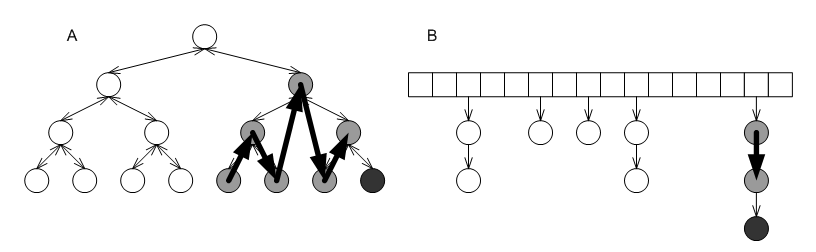
Figure Point-type iterators in hash tables-A shows the simplest (and most efficient) implementation of a collision-chaining hash table. The little box marked point_iterator shows an object that contains a pointer to the element's node. Note that this "iterator" has no way to move to the next element (i.e., it cannot support operator++). Conversely, the little box marked iterator stores both a pointer to the element, as well as some other information (e.g., the bucket number of the element). the second iterator, then, is "heavier" than the first one- it requires more time and space. If we were to use a different container to cross-reference into this hash-table using these iterators - it would take much more space. As noted in Using Point-Type Iterators for Range-Type Operations, nothing much can be done by incrementing these iterators, so why is this extra information needed?

Alternatively, one might create a collision-chaining hash-table where the lists might be linked, forming a monolithic total-element list, as in Figure Point-type iterators in hash tables-B (this seems similar to the Dinkumware design [dinkumware_stl]). Here the iterators are as light as can be, but the hash-table's operations are more complicated.

Point-type iterators in hash tables.

It should be noted that containers based on collision-chaining hash-tables are not the only ones with this type of behavior; many other self-organizing data structures display it as well.

Invalidation Guarantees

Consider the following snippet:

it = c.find(3);

c.erase(5);

Following the call to erase, what is the validity of it: can it be de-referenced? can it be incremented?

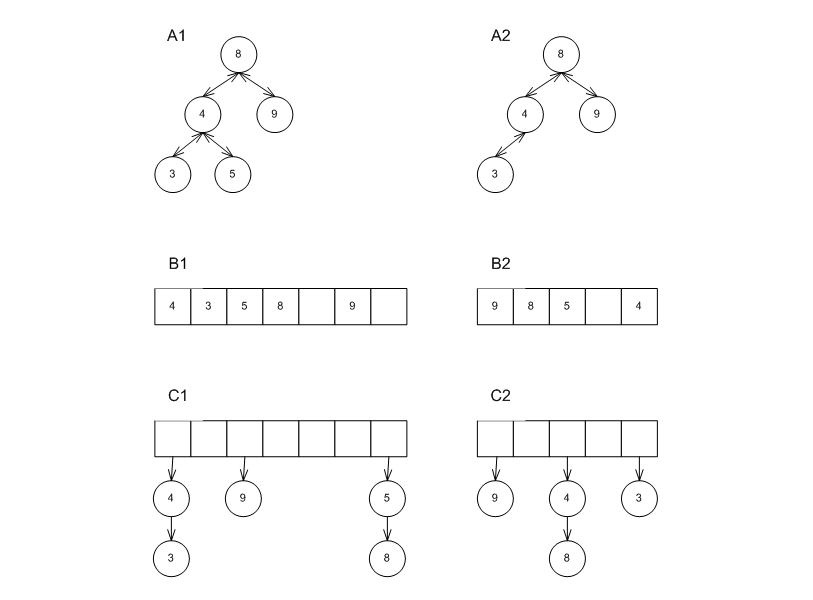
The answer depends on the underlying data structure of the container. Figure Effect of erase in different underlying data structures shows three cases: A1 and A2 show a red-black tree; B1 and B2 show a probing hash-table; C1 and C2 show a collision-chaining hash table.

Effect of erase in different underlying data structures.

Erasing 5 from A1 yields A2. Clearly, an iterator to 3 can be de-referenced and incremented. The sequence of iterators changed, but in a way that is well-defined by the interface.
Erasing 5 from B1 yields B2. Clearly, an iterator to 3 is not valid at all - it cannot be de-referenced or incremented; the order of iterators changed in a way that is (practically) determined by the implementation and not by the interface.
Erasing 5 from C1 yields C2. Here the situation is more complicated. On the one hand, there is no problem in de-referencing it. On the other hand, the order of iterators changed in a way that is (practically) determined by the implementation and not by the interface.

So in classic STL, it is not always possible to express whether it is valid or not. This is true also for insert, e.g.. Again, the iterator concept seems overloaded.

Slightly Different Methods

[meyers02both] points out that a class's methods should comprise only operations which depend on the class's internal structure; other operations are best designed as external functions. Possibly, therefore, the STL's associative containers lack some useful methods, and provide some other methods which would be better left out (e.g., [sgi_stl] ).

Methods Related to Erase

Order-preserving STL associative containers provide the method
```
iterator 
    erase
    (iterator it)
```
which takes an iterator, erases the corresponding element, and returns an iterator to the following element. Also hash-based STL associative containers provide this method. This seemingly increases genericity between associative containers, since, e.g., it is possible to use
```
typename C::iterator it = c.begin();
typename C::iterator e_it = c.end();

while(it != e_it)
    it = pred(*it)? c.erase(it) : ++it;
```
in order to erase from a container object c all element which match a predicate pred. However, in a different sense this actually decreases genericity: an integral implication of this method is that tree-based associative containers' memory use is linear in the total number of elements they store, while hash-based containers' memory use is unbounded in the total number of elements they store. Assume a hash-based container is allowed to decrease its size when an element is erased. Then the elements might be rehashed, which means that there is no "next" element - it is simply undefined. Consequently, it is possible to infer from the fact that STL hash-based containers provide this method that they cannot downsize when elements are erased (Performance Tests::Hash-Based Container Tests quantifies this.) As a consequence, different code is needed to manipulate different containers, assuming that memory should be conserved. pb_ds's non-order preserving associative containers omit this method.
All of pb_ds's associative containers include a conditional-erase method
```
template<
    class Pred>
size_type
    erase_if
    (Pred pred)
```
which erases all elements matching a predicate. This is probably the only way to ensure linear-time multiple-item erase which can actually downsize a container.
STL associative containers provide methods for multiple-item erase of the form
```
size_type
    erase
    (It b, 
        It e)
```
erasing a range of elements given by a pair of iterators. For tree-based or trie-based containers, this can implemented more efficiently as a (small) sequence of split and join operations. For other, unordered, containers, this method isn't much better than an external loop. Moreover, if c is a hash-based container, then, e.g., c.erase(c.find(2), c.find(5)) is almost certain to do something different than erasing all elements whose keys are between 2 and 5, and is likely to produce other undefined behavior.

Methods Related to Split and Join

It is well-known that tree-based and trie-based container objects can be efficiently split or joined [clrs2001]. Externally splitting or joining trees is super-linear, and, furthermore, can throw exceptions. Split and join methods, consequently, seem good choices for tree-based container methods, especially, since as noted just before, they are efficient replacements for erasing sub-sequences. Performance Tests::Tree-Like-Based Container Tests quantifies this.

Methods Related to Insert

STL associative containers provide methods of the form

template<
    class It>
size_type
    insert
    (It b,
        It e);

for inserting a range of elements given by a pair of iterators. At best, this can be implemented as an external loop, or, even more efficiently, as a join operation (for the case of tree-based or trie-based containers). Moreover, these methods seem similar to constructors taking a range given by a pair of iterators; the constructors, however, are transactional, whereas the insert methods are not; this is possibly confusing.

Functions Related to Comparison

Associative containers are parametrized by policies allowing to test key equivalence; e.g. a hash-based container can do this through its equivalence functor, and a tree-based container can do this through its comparison functor. In addition, some STL associative containers have global function operators, e.g., operator== and operator<=, that allow comparing entire associative containers.

In our opinion, these functions are better left out. To begin with, they do not significantly improve over an external loop. More importantly, however, they are possibly misleading - operator==, for example, usually checks for equivalence, or interchangeability, but the associative container cannot check for values' equivalence, only keys' equivalence; also, are two containers considered equivalent if they store the same values in different order? this is an arbitrary decision.

Alternative to Multiple Equivalent Keys

Maps (or sets) allow mapping (or storing) unique-key values. The STL, however, also supplies associative containers which map (or store) multiple values with equivalent keys: std::multimap, std::multiset, std::tr1::unordered_multimap, and unordered_multiset. We first discuss how these might be used, then why we think it is best to avoid them.

Suppose one builds a simple bank-account application that records for each client (identified by an std::string) and account-id (marked by an unsigned long) - the balance in the account (described by a float). Suppose further that ordering this information is not useful, so a hash-based container is preferable to a tree based container. Then one can use

std::tr1::unordered_map<std::pair<std::string, unsigned long>, float, ...>

which hashes every combination of client and account-id. This might work well, except for the fact that it is now impossible to efficiently list all of the accounts of a specific client (this would practically require iterating over all entries). Instead, one can use

std::tr1::unordered_multimap<std::pair<std::string, unsigned long>, float, ...>

which hashes every client, and decides equivalence based on client only. This will ensure that all accounts belonging to a specific user are stored consecutively.

Also, suppose one wants an integers' priority queue (i.e., a container that supports push, pop, and top operations, the last of which returns the largest int) that also supports operations such as find and lower_bound. A reasonable solution is to build an adapter over std::set<int>. In this adapter, e.g., push will just call the tree-based associative container's insert method; pop will call its end method, and use it to return the preceding element (which must be the largest). Then this might work well, except that the container object cannot hold multiple instances of the same integer (push(4), e.g., will be a no-op if 4 is already in the container object). If multiple keys are necessary, then one might build the adapter over an std::multiset<int>.

STL non-unique-mapping containers, then, are useful when (1) a key can be decomposed in to a primary key and a secondary key, (2) a key is needed multiple times, or (3) any combination of (1) and (2).

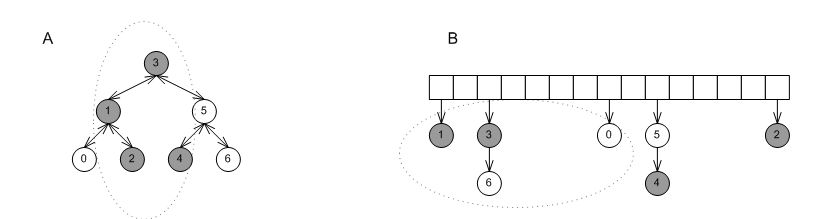
Figure Non-unique mapping containers in the STL's design shows how the STL's design works internally; in this figure nodes shaded equally represent equivalent-key values. Equivalent keys are stored consecutively using the properties of the underlying data structure: binary search trees (Figure Non-unique mapping containers in the STL's design-A) store equivalent-key values consecutively (in the sense of an in-order walk) naturally; collision-chaining hash tables (Figure Non-unique mapping containers in the STL's design-B) store equivalent-key values in the same bucket, the bucket can be arranged so that equivalent-key values are consecutive.

Non-unique mapping containers in the STL's design.

Put differently, STL non-unique mapping associative-containers are associative containers that map primary keys to linked lists that are embedded into the container. Figure Effect of embedded lists in STL multimaps shows again the two containers from Figure Non-unique mapping containers in the STL's design, this time with the embedded linked lists of the grayed nodes marked explicitly.

Effect of embedded lists in STL multimaps.

These embedded linked lists have several disadvantages.

The underlying data structure embeds the linked lists according to its own consideration, which means that the search path for a value might include several different equivalent-key values. For example, the search path for the the black node in either of Figures Non-unique mapping containers in the STL's design A or B, includes more than a single gray node.
The links of the linked lists are the underlying data structures' nodes, which typically are quite structured. E.g., in the case of tree-based containers (Figure Effect of embedded lists in STL multimaps-B), each "link" is actually a node with three pointers (one to a parent and two to children), and a relatively-complicated iteration algorithm. The linked lists, therefore, can take up quite a lot of memory, and iterating over all values equal to a given key (e.g., through the return value of the STL's equal_range) can be expensive.
The primary key is stored multiply; this uses more memory.
Finally, the interface of this design excludes several useful underlying data structures. E.g., of all the unordered self-organizing data structures, practically only collision-chaining hash tables can (efficiently) guarantee that equivalent-key values are stored consecutively.

The above reasons hold even when the ratio of secondary keys to primary keys (or average number of identical keys) is small, but when it is large, there are more severe problems:

The underlying data structures order the links inside each embedded linked-lists according to their internal considerations, which effectively means that each of the links is unordered. Irrespective of the underlying data structure, searching for a specific value can degrade to linear complexity.
Similarly to the above point, it is impossible to apply to the secondary keys considerations that apply to primary keys. For example, it is not possible to maintain secondary keys by sorted order.
While the interface "understands" that all equivalent-key values constitute a distinct list (e.g., through equal_range), the underlying data structure typically does not. This means, e.g., that operations such as erasing from a tree-based container all values whose keys are equivalent to a a given key can be super-linear in the size of the tree; this is also true also for several other operations that target a specific list.

In pb_ds, therefore, all associative containers map (or store) unique-key values. One can (1) map primary keys to secondary associative-containers (i.e., containers of secondary keys) or non-associative containers (2) map identical keys to a size-type representing the number of times they occur, or (3) any combination of (1) and (2). Instead of allowing multiple equivalent-key values, pb_ds supplies associative containers based on underlying data structures that are suitable as secondary associative-containers (see Associative-Container Performance Tests::Observations::Mapping-Semantics Considerations).

Figures Non-unique mapping containers in pb_ds A and B show the equivalent structures in pb_ds's design, to those in Figures Non-unique mapping containers in the STL's design A and B, respectively. Each shaded box represents some size-type or secondary associative-container.

Non-unique mapping containers in the `pb_ds`.

In the first example above, then, one would use an associative container mapping each user to an associative container which maps each application id to a start time (see basic_multimap.cc); in the second example, one would use an associative container mapping each int to some size-type indicating the number of times it logically occurs (see basic_multiset.cc).

Associative-Container Performance Tests::Multimaps quantifies some of these points, and Associative-Container Performance Tests::Observations::Mapping-Semantics Considerations shows some simple calculations.

Associative-Container Examples::Multimaps shows some simple examples of using "multimaps".

Design::Associative Containers::List-Based Containers discusses types of containers especially suited as secondary associative-containers.

Priority Queues

Slightly Different Methods

Priority queues are containers that allow efficiently inserting values and accessing the maximal value (in the sense of the container's comparison functor); i.e., their interface supports push and pop. The STL's priority queues indeed support these methods, but they support little else. For algorithmic and software-engineering purposes, other methods are needed:

Many graph algorithms [clrs2001] require increasing a value in a priority queue (again, in the sense of the container's comparison functor), or joining two priority-queue objects.
It is sometimes necessary to erase an arbitrary value in a priority queue. For example, consider the select function for monitoring file descriptors:
```
int 
    select
    (int nfds,             
        fd_set *readfds,                
        fd_set *writefds,
        fd_set *errorfds, 
        struct timeval *timeout);
```
then, as the select manual page [select_man] states:
The nfds argument specifies the range of file descriptors to be tested. The select() function tests file descriptors in the range of 0 to nfds-1.

It stands to reason, therefore, that we might wish to maintain a minimal value for nfds, and priority queues immediately come to mind. Note, though, that when a socket is closed, the minimal file description might change; in the absence of an efficient means to erase an arbitrary value from a priority queue, we might as well avoid its use altogether.

Priority-Queue Examples::Cross-Referencing shows examples for these types of operations.
STL containers typically support iterators. It is somewhat unusual for std::priority_queue to omit them (see, e.g., [meyers01stl]). One might ask why do priority queues need to support iterators, since they are self-organizing containers with a different purpose than abstracting sequences. There are several reasons:
1. Iterators (even in self-organizing containers) are useful for many purposes, e.g., cross-referencing containers, serialization, and debugging code that uses these containers.
2. The STL's hash-based containers support iterators, even though they too are self-organizing containers with a different purpose than abstracting sequences.
3. In STL-like containers, it is natural to specify the interface of operations for modifying a value or erasing a value (discussed previously) in terms of a iterators. This is discussed further in Design::Priority Queues::Iterators. It should be noted that the STL's containers also use iterators for accessing and manipulating a specific value. E.g., in hash-based containers, one checks the existence of a key by comparing the iterator returned by find to the iterator returned by end, and not by comparing a pointer returned by find to NULL.

Performance Tests::Priority Queues quantifies some of these points.

More Data Structures and Traits

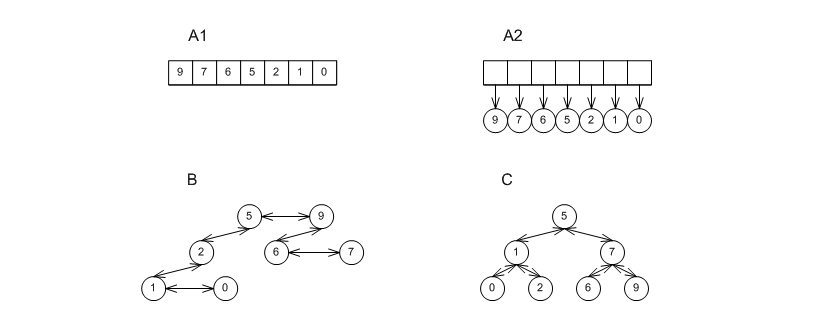
There are three main implementations of priority queues: the first employs a binary heap, typically one which uses a sequence; the second uses a tree (or forest of trees), which is typically less structured than an associative container's tree; the third simply uses an associative container. These are shown, respectively, in Figures Underlying Priority-Queue Data-Structures A1 and A2, B, and C.

Underlying Priority-Queue Data-Structures.

No single implementation can completely replace any of the others. Some have better push and pop amortized performance, some have better bounded (worst case) response time than others, some optimize a single method at the expense of others, etc.. In general the "best" implementation is dictated by the problem (see Performance Tests::Priority Queues::Observations).

As with associative containers (see Associative Containers::Traits for Underlying Data-Structures), the more implementations co-exist, the more necessary a traits mechanism is for handling generic containers safely and efficiently. This is especially important for priority queues, since the invalidation guarantees of one of the most useful data structures - binary heaps - is markedly different than those of most of the others.

Design::Priority Queues::Traits discusses this further.

Binary Heap Implementation

Binary heaps are one of the most useful underlying data structures for priority queues. They are very efficient in terms of memory (since they don't require per-value structure metadata), and have the best amortized push and pop performance for primitive types (e.g., ints).

The STL's priority_queue implements this data structure as an adapter over a sequence, typically std::vector or std::deque, which correspond to Figures Underlying Priority-Queue Data-Structures A1 and A2, respectively.

This is indeed an elegant example of the adapter concept and the algorithm/container/iterator decomposition (see [nelson96stlpql]). There are possibly reasons, however, why a binary-heap priority queue would be better implemented as a container instead of a sequence adapter:

std::priority_queue cannot erase values from its adapted sequence (irrespective of the sequence type). This means that the memory use of an std::priority_queue object is always proportional to the maximal number of values it ever contained, and not to the number of values that it currently contains (see Priority Queue Text pop Memory Use Test); this implementation of binary heaps acts very differently than other underlying data structures (e.g., pairing heaps).
Some combinations of adapted sequences and value types are very inefficient or just don't make sense. If one uses std::priority_queue<std::vector<std::string> > >, for example, then not only will each operation perform a logarithmic number of std::string assignments, but, furthermore, any operation (including pop) can render the container useless due to exceptions. Conversely, if one uses std::priority_queue<std::deque<int> > >, then each operation uses incurs a logarithmic number of indirect accesses (through pointers) unnecessarily. It might be better to let the container make a conservative deduction whether to use the structure in Figures Underlying Priority-Queue Data-Structures A1 or A2.
There does not seem to be a systematic way to determine what exactly can be done with the priority queue.
1. If p is a priority queue adapting an std::vector, then it is possible to iterate over all values by using &p.top() and &p.top() + p.size(), but this will not work if p is adapting an std::deque; in any case, one cannot use p.begin() and p.end(). If a different sequence is adapted, it is even more difficult to determine what can be done.
2. If p is a priority queue adapting an std::deque, then the reference return by p.top() will remain valid until it is popped, but if p adapts an std::vector, the next push will invalidate it. If a different sequence is adapted, it is even more difficult to determine what can be done.
Sequence-based binary heaps can still implement linear-time erase and modify operations. This means that if one needs, e.g., to erase a small (say logarithmic) number of values, then one might still choose this underlying data structure. Using std::priority_queue, however, this will generally change the order of growth of the entire sequence of operations.